앞서 XOR operation은 단일 레이어로
정답을 유추하기에 어려움이 있다고 언급하였다.
따라서 다중레이어 즉, multilayer를 사용해야 하는데
레이어가 증가할 수록 새롭게 정의해야 하는 weight값과 bias값이
증가한다는 문제점도 있다고 언급하였다.
XOR 연산 풀어보기
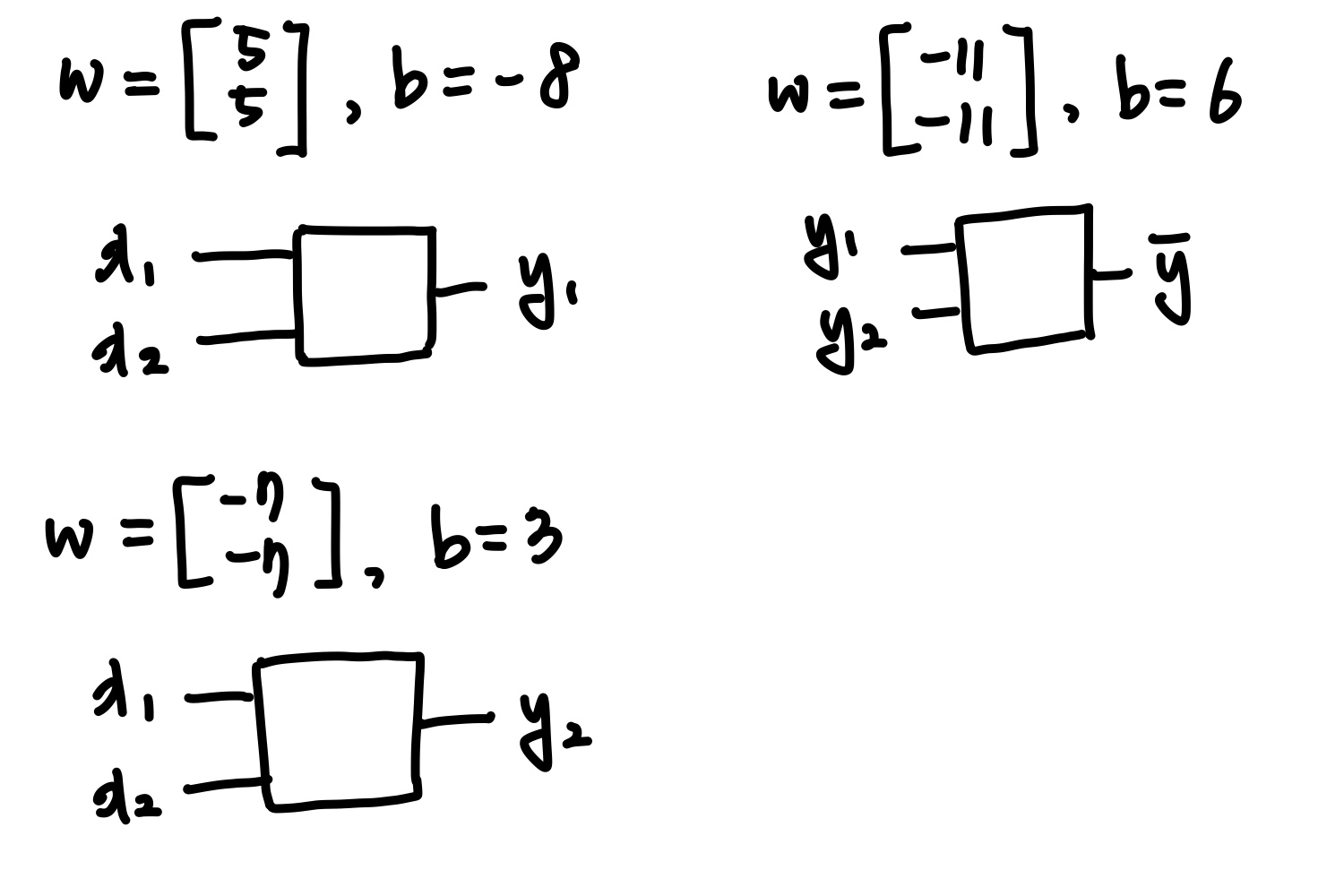
3개의 unit의 weight와 bias를 임의로 설정하여 XOR연산을 풀이해보겠다.
x1, x2의 입력을 넣어 각 y1, y2의 결과를 도출하고
y1, y2의 입력을 넣어 ȳ의 결과를 도출하게 한다.
이때, ȳ가 XOR연산의 결과가 되는 것이다.
각 레이어는 아래와 같이 계산한다.
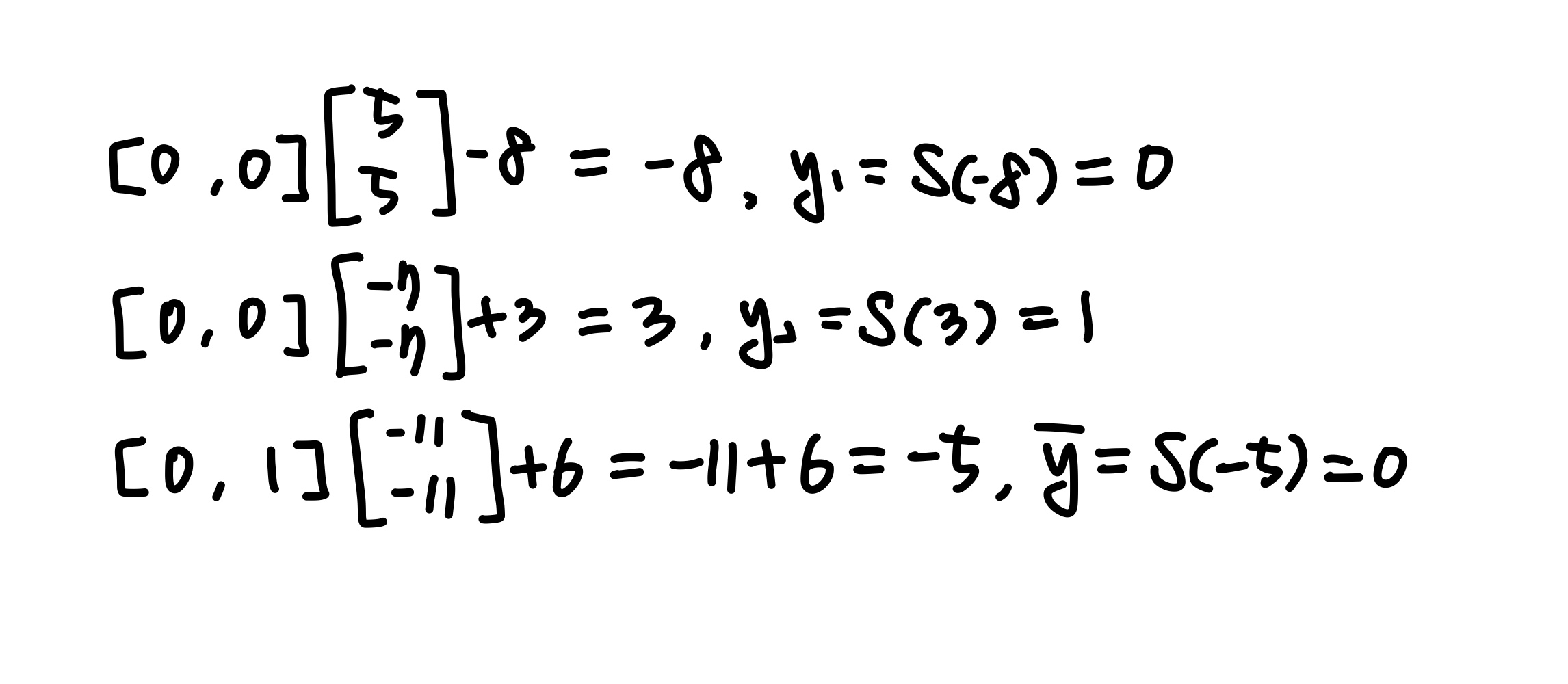
이때 각 값을 구하는 S함수는 sigmoid함수로 앞서 언급하였다.
단순히 음수면 0의 값을, 양수면 1의 값을 도출한다고 생각해도 좋다.
첫 번째와 두 번째 유닛애는 x1, x2의 값을 넣었고,
세 번째 식에서는 각 유닛의 연산 결과인 y1, y2를 넣었다.
모든 경우의 수를 넣어 계산한 결과는 아래와 같다.
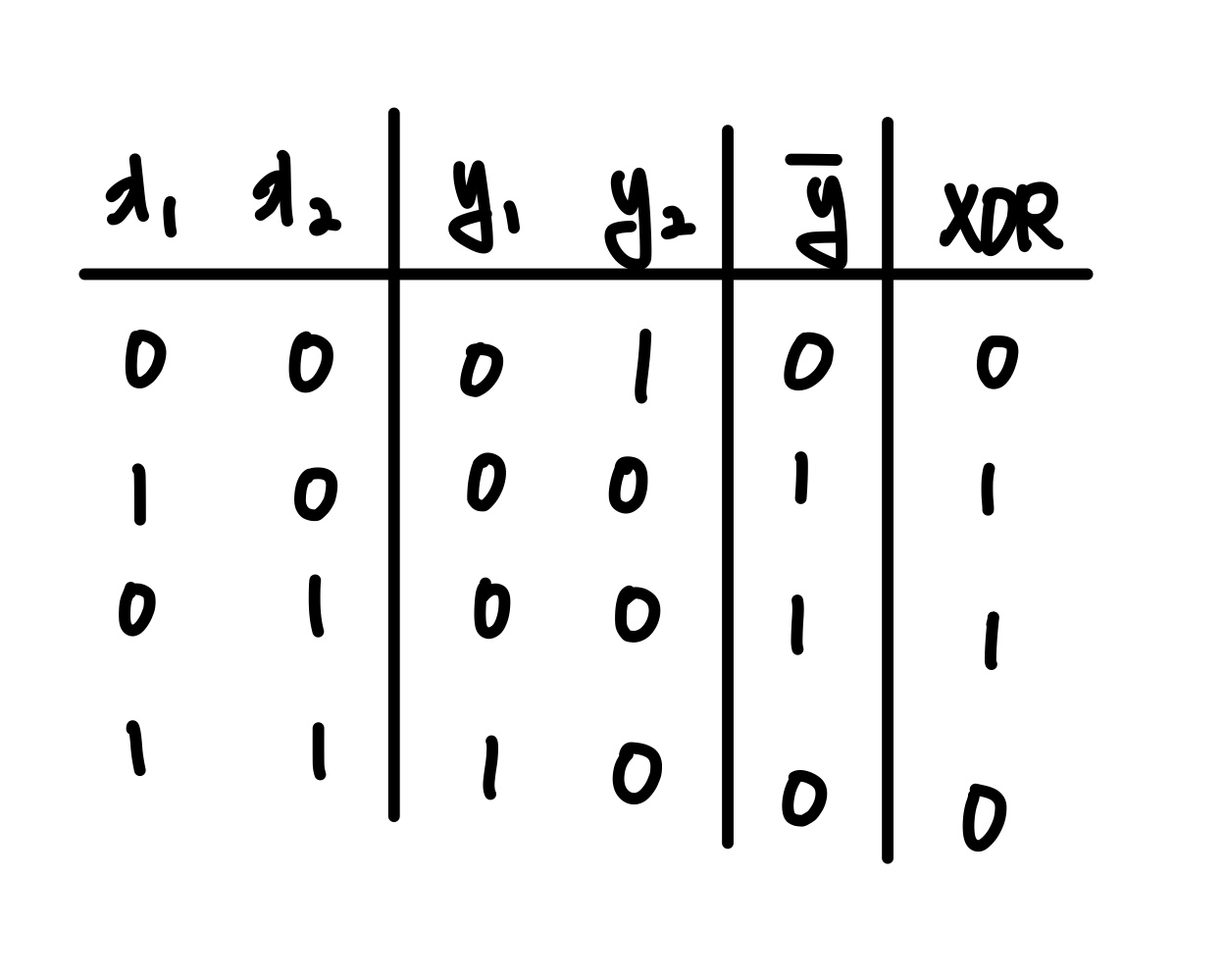
위의 unit을 하나로 뭉쳐서 그리면 아래와 같다.

이때 각 unit은 gate또는 Perceptron이라고도 한다.
이러한 유닛들의 집합을 Neural Network라고 한다.
그런데, 위와 같은 생김새는 우리가 어디서 본 적이 있는 것 같다.
바로 이전에 학습한 multinomial classification과 유사하다.
따라서 우리는 각 perceptron의 weight값과 bias값을 합쳐
하나의 행렬로 표현하여 계산할 수 있다.
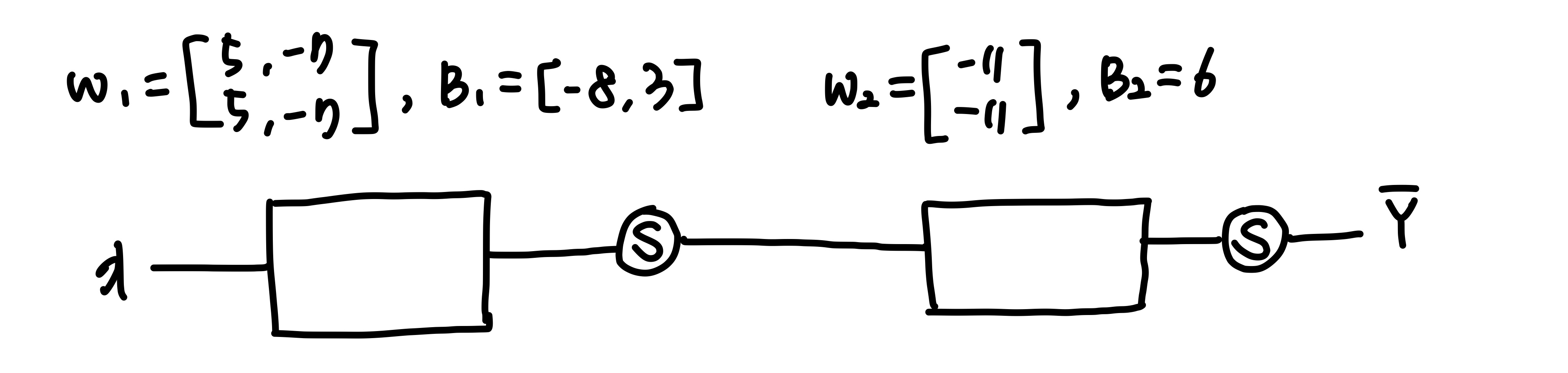
위의 그림을 수식으로 쓰면 아래와 같다.
이때 K는 첫 번째 perceptron의 결과값을 이야기한다.
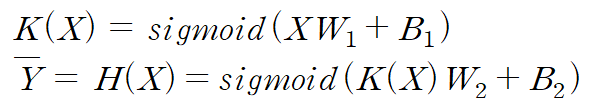
이때 W1, B1, W2, B2의 값은 어떻게 구할 수 있을까?
Backpropagation
사실은 가장 처음의 W와 B의 값을 랜덤으로 결정한다.
이후 backpropagation 방법을 사용하여 파라미터의 값을 조정하는데
이러한 방법은 gradient descent algorithm와 비슷하다.
backpropagation을 이해하기 위해 간단한 예를 들어보겠다.
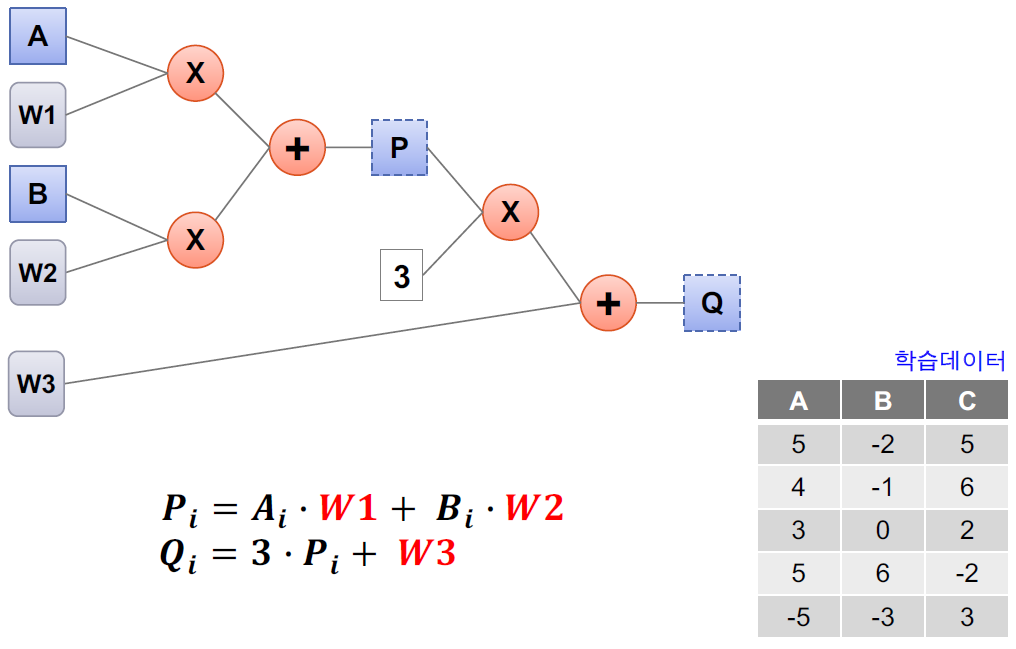
위 그림에서 A와 B는 입력값, C는 결과로 도출되어야 하는 결과값이다.
W1, W2, W3은 각 weight값이다. backpropagation을 통해 각 weight값을 조정하자.
앞서 우리는 경사하강법을 사용할 때 loss function 또는 cost function의
기울기를 구하여 해당 기울기가 0에 수렴하는 방향으로
weight를 조정하였다.
backpropagation 방법도 마찬가지이다.
loss function을 구하여 해당 함수의 기울기가 작아지는 방향으로 조정한다.
위 예시에서의 loss function은 아래와 같다.

앞에서 1/2을 곱해주는 이유는 기울기를 구하기 위해서는
미분을 해주어야 하는데 제곱식을 미분할 때 발생하는
2를 없애 계산을 간결하게 하기 위함으로 없어도 무관하다.

각 W1, W2, W3의 값을 임의로 1.0, 1.0, -1.0로 설정하였다.
이제부터 적당한 weight를 backpropagation으로 찾아 나갈 것이다.
A가 5, B가 -1일 때, 해당 weight를 통해 연산한 Q의 값은 8.0이 된다.
이때 Q와 C의 차는 3.0이다. (예측 값이 5여야 하므로)
이제 loss function을 통해 경사하강법으로 값을 조정해보자.
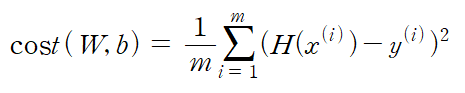
이전에 우리가 학습한 cost function은 위와 같다.
각각의 파라미터의 값을 조정할 때에
아래와 같은 방법을 통하여 각각의 파라미터 값을 조정하였다.

backpropagation도 마찬가지이다.
하지만, layer의 개수가 많아진다면 계산해야 할 식도 길어진다.

앞서 제시한 예시에서 파라미터를 구하기 위해 식을 위와 같이 변형해야 한다.
현재는 레이어가 많지 않아 간결해 보이지만 레이어의 개수가 많아지면
위와 같은 식도 엄청나게 길어질 것이다.
이러한 문제를 해결하기 위하여 우리는 Chain Rule을 사용할 것이다.
Chain Rule이란 미분 시에 도함수에 대한 미분이라고 생각하면 쉽다.
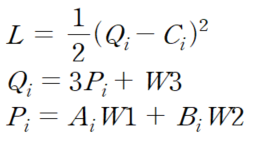
위와 같은 식일 때 각 weight를 구하기 위해서는
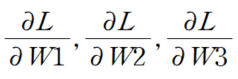
위와 같은 식을 사용해야 하는데,
Chain Rule을 적용하면
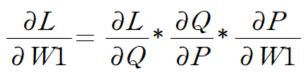
와 같이 표현할 수 있다.
즉, 각 식에서 해당 변수에 대해서만 미분하면 되는 것이다.
'Computer Science > 기계학습 (Machine Learning)' 카테고리의 다른 글
| [머신러닝/ML] Dropout과 Ensemble, 네트워크 쌓기 (0) | 2023.07.26 |
|---|---|
| [머신러닝/ML] ReLU와 Weight 초기화 (0) | 2023.07.26 |
| [머신러닝/ML] 딥러닝의 기본 개념 (0) | 2023.07.20 |
| [머신러닝/ML] Training Set, Testing Set (0) | 2023.05.22 |
| [머신러닝/ML] Learning Rate, Data Preprocessing, Overfiting (0) | 2023.05.20 |