Softmax Classification / Multinomial Classification
앞서 우리가 학습한 Binary Classification은 0이냐 1이냐를 예측하는 문제였다.
이번 시간에 학습할 Softmax Classification은 0이나 1 뿐만 아니라,
즉 2개 이상인 결과값을 예측할 때 쓰인다.
Softmax Classification을 위한 새로운 예를 가져와보겠다.

공부 시간과 출석률에 따른 성적을 예측하는 모델이다.
결과값은 A, B, C로 2개 이상이다. 이를 예측하기 위해 어떤 알고리즘을 사용하는 것이 좋을까.
앞선 시간에 학습했던 Binary Classification을 활용하여 해당 값이 A인지 아닌지, B인지 아닌지만 판별해보자.
각각을 분류할 수 있는 직선을 그어보면 아래와 같이 나온다.
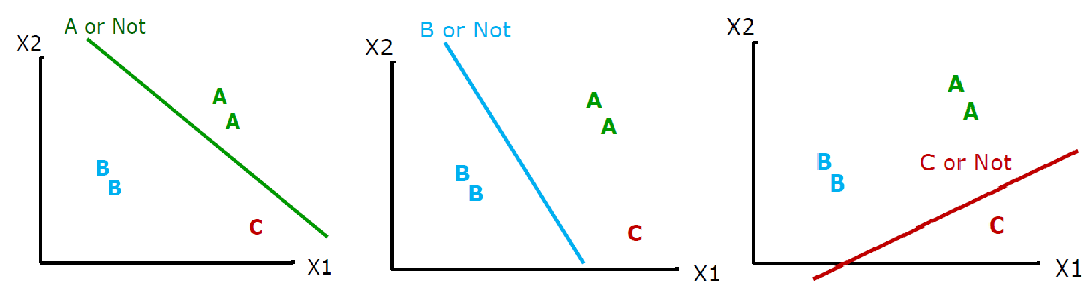
우리는 각 3개의 직선을 만들어 냈기 때문에 각 3개의 독립적인 벡터로 직선을 나타냈다.
식으로 표현하면 아래와 같다.

하지만 위와 같이 각각 독립적인 벡터로 표현하면 최종적인 클래스를 결정할 때 문제가 생길 수 있다.
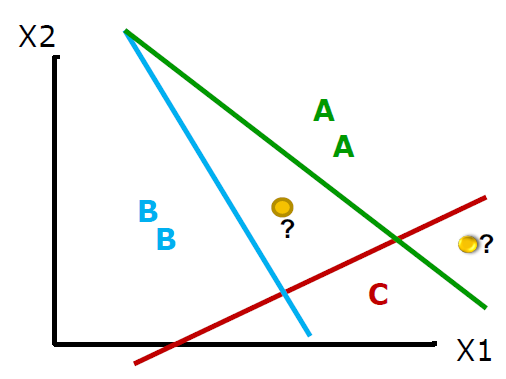
위 그림은 작성한 모든 그래프를 한 평면 위에 나타낸 것인데, 노란색 점으로 표시된 곳에
새로운 데이터 들어왔을 때 해당 데이터에 대해 어떻게 예측해야 하는지에 대한 값이 모호하기 때문이다.
따라서, 똑똑한 사람은 각 벡터를 아래와 같은 과정을 통해 하나의 행렬로 표현하기로 하였다.
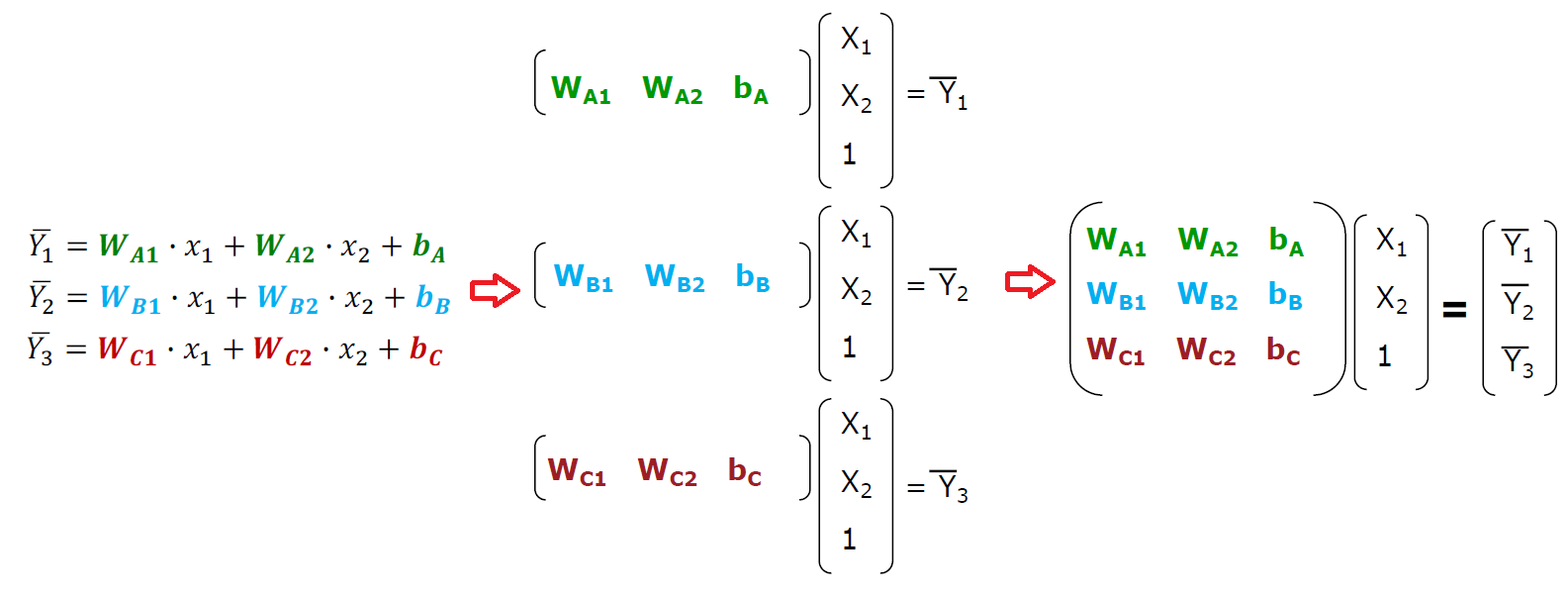
위의 ȳ는 Y bar 또는 Y hat이라고 하며 H(x) 연산의 결과값이다.
데이터에서 정답(결과값으로 예측되어야 하는 값)과 구분하기 위해 hat을 붙여주었다.
행렬을 통해 값을 한 번에 계산시킬 수 있을 뿐더러, 각 값을 독립된 값처럼 계산할 수 있다.
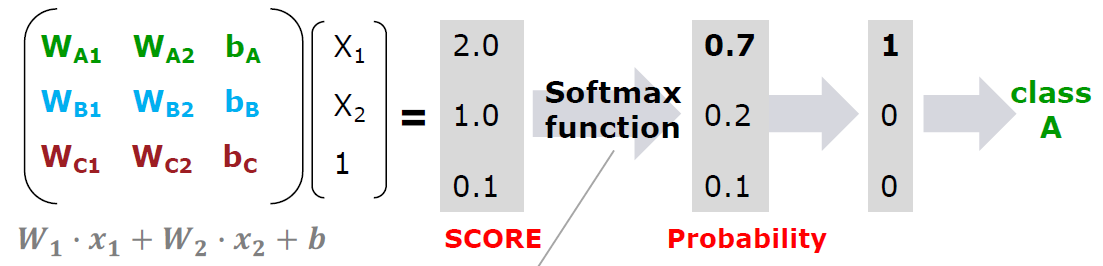
위의 행렬에 어떤 데이터를 넣어 값을 비교하면 각 2.0, 1.0, 0.1의 값이 나온다.
나온 결과를 통해 ȳ는 A인 것을 확인할 수 있지만, 우리는 결과값이 확률로 나오길 원한다.
이때 어떠한 함수에 해당 값을 넣으면 확률값이 나오게 되고, 각 값을 모두 더하면 1이 된다.
이 어떠한 함수는 Softmax Function이다.
Soft Function은 아래와 같이 표현할 수 있다.

따라서 위의 예시에서 A일 확률이 0.7이고, B일 확률이 0.2, C일 확률이 0.1이 되는 것이다.
해당 확률을 통해 ȳ의 값이 어떤 클래스인지를 나타낼 때 One-Hot-Encoding라는 방법을 사용한다.
Cross-Entropy
우리는 Softmax Classification Cost Function을 구하기 위해 Cross-Entropy를 사용한다.
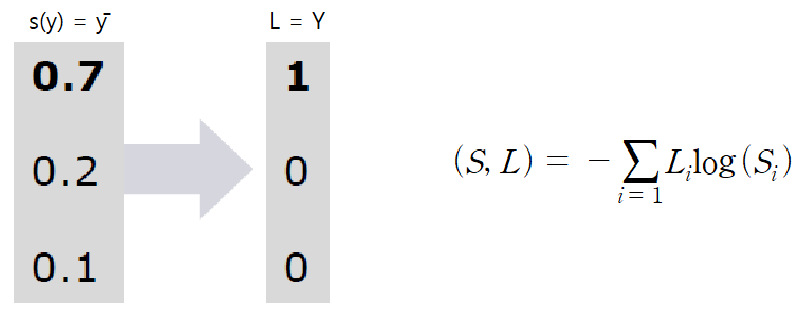
ȳ값을 S, y의 값을 L이라고 했을 때 Cross-Entropy통해 구한 함수는 위 그림의 우측처럼 나타낼 수 있다.
위 식을 재정의하면 아래와 같이 나타낼 수 있다.
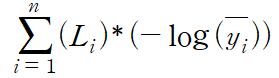

위 사진은 y = B이고, 예측된 값에 따라 cross entropy를 통해 어떠한 값이 나오는지를 계산한 모습이다.
재정의된 식을 바탕으로 계산한 것이며, 각 벡터의 곱은 외적곱(element-wise multiplication)임을 유의하자.
ȳ가 A = 0, B = 1로 예측했을 때 log함수에서는 각 A, B값에 대해 무한대의 값과, 0의 값을 가지며
이들을 ȳ와 외적곱을 했을 때 0의 값이 나와 옳은 판단이라고 할 수 있다.
반대로, ȳ가 A = 1, B = 0으로 예측했을 때 log함수에서는 각 A, B값에 대해 0의 값과, 무한대의 값을 가지며
이들을 ȳ와 외적곱을 했을 때 무한대의 값이 나와 비용이 매우 크므로 잘못된 판단이라고 할 수 있다.
각 cost를 평균을 내면 아래 식과 같아진다.
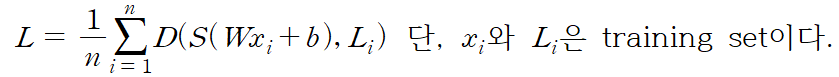
이도 마찬가지로 경사하강법을 이용하여 최소값을 구할 수 있다.
'Computer Science > 기계학습 (Machine Learning)' 카테고리의 다른 글
| [머신러닝/ML] Training Set, Testing Set (0) | 2023.05.22 |
|---|---|
| [머신러닝/ML] Learning Rate, Data Preprocessing, Overfiting (0) | 2023.05.20 |
| [머신러닝/ML] Binary Classification / Logistic Regression (0) | 2023.05.18 |
| [머신러닝/ML] Multivariable Linear Regression (0) | 2023.05.18 |
| [머신러닝/ML]Linear Regression (선형회귀) (0) | 2023.05.15 |