본 포스트는 2024년 봄 학기 충남대학교 이종률 교수님의 데이터 과학 강의 정리자료입니다.
Data Preprocessing
데이터 전처리가 필요한 이유는 현실 세계에 존재하는 데이터를 바로 가져다 쓰기엔 결함이 많기 때문이다. 결함의 종류에 대해 알아보자.
imcomplete
어떤 속성값이 부족한 경우가 존재한다.
noisy
오류나 outlier값을 가진 경우가 존재한다. 예를 들어 급여 항목에 음수값이 들어가 있는 경우이다.
inconsistent
코드나 이름에 일치되지 않는 값이 존재한다. 예를 들어 어떤 rank에 대해 A, B, C로 표기했던 것을 1, 2, 3으로 바꿔 표시한 경우도 해당된다.
데이터가 중복되거나 누락되는 경우 부정확하거나 오해의 소지가 있는 통계 결과는 낼 수 있다. 따라서 데이터의 품질에 대해 다차원적으로 평가해야 한다.
대부분 받아들여지는 관점으로는 accuracy, completeness, consistency, timeliness, believability, value added, interpretability, accessibility가 있다.
Major tasks
데이터 전처리 시에 할 수 잇는 주요한 task들은 아래와 같다.
Data Cleaning
missing data를 채우고, outlier놔 noise를 제거하는 과정이다.
Data Integration
데이터의 소스가 여러 개인 경우, 데이터 베이스나 파일들을 엮는(합치는) 과정이다.
Data Transformation
데이터를 집계하고 정규화하는 과정이다. 모델링의 편의성을 위한 과정이다.
Data Reduction
주어진 데이터가 너무 많을 때, 부득이하게 데이터의 정확성을 조금 잃어버리지만 heuristics한 결과를 얻기 위해 필요 없는 데이터의 일부를 삭제하는 과정이다.
Data Discretization
데이터가 continuous한 경우 그 데이터 자체를 표현하기에 어려움이 존재하기 때문에 데이터를 분석 가능한 형태로, 즉 데이터를 이산적으로 바꿔주는 과정이다.
Key Data Properties to EDA (EDA의 주요 데이터 속성)
Structure
데이터 파일의 모양을 우리는 "structure"라고 한다. 이때, 데이터의 각 타입이나, 저장된 모습에 대해 말한다.

위 사진은 variable feature type의 관점에서 데이터를 분류한 모습이다. 왼쪽의 경우 양적으로 나눈 경우인데, 값이 연속적인지 이산적인지에 대해 나눌 수 있다. 오른쪽의 경우 질적으로 나눈 경우이며, 값이 순서적(ordinal)이거나, 그렇지 않거나에 대해 나눌 수 있다.
따라서 structure는 데이터를 표현하는 format도 고려대상이 되는데, 데이터가 Tabular(테이블형)인 경우 CSV, TSV, 엑셀, SQL과 같이 나타낼 수 있다. 또한 데이터가 Nested(중첩)인 경우 JSON이나 XML을 주로 사용한다.
Granularity (세분성)
우리는 각 데이터가 fine(미세)하거나 coarse(거친)한 정도를 나타내는 지를 확인할 수 있다. 즉, 데이터가 각 개인을 나타내는 것인지, 작은 그룹 또는, 큰 그룹을 나타내는 것인지 확인할 수 있다.
각 record가 동등한 granularity를 가지고 있는지를 확인해야 한다. 즉, 어떤 record는 개인인데, 다른 record는 그룹을 나타내면 안 된다는 의미이다. 이때, 레코드가 coarse한 경우 대표값이 어떻게 계산되는지에 대해 봐야 한다.
Scope
scope는 데이터의 관점에서 원하는 정보의 범위를 잘 포함하고 있는지 확인하는 것이다. 또는 데이터가 너무 많은 경우 필요 없는 데이터를 필터링 하도록 판단하는 과정이다. 또한 현재 가지고 있는 데이터의 기간이 적절한지도 판단할 수 있다.
Temporality
내가 조사하려는 타겟 데이터가 변화할 여지가 있는지, 또는 데이터가 어떤 주기성을 가지는지 확인할 수 있다. 이때, 시간에 따른 분석 시 취할 수 있는 action도 변화할 수 있다. 예를 들어 자동차의 교통량와 같은 데이터를 조사할 때, 출퇴근 시간이나 아침, 밤 시간과 같이 시간대 별로 분석이 달라질 수 있다.
즉, 어떤 시간의 변화를 가지고 데이터 분석에 반영하는 것을 Temporality라고 한다.
Faithfulness (데이터 충실도)
데이터가 현재의 상황을 얼마나 잘 표현, 반영하고 있는지에 대한 평가이다.
- artificial한 값이 들어가 있는지.
- 실제 벌어지지 않은 데이터가 들어가 있는지.
- 양수의 데이터만 존재하는 속성에 대해 음수가 들어가 있는지.
- 이름의 스펠링이 잘못 되어 있다던지.
- outlier가 크다던지.
위와 같은 내용을 고려해야 한다.
또한, 의존성이 있는 데이터가 잘못된 경우, 예를 들어 생년월일과 나이가 맞지 않은 경우. 또는 데이터 위조에 대한 징후가 있는 경우, 예를 들어 동일한 이름이 존재한다거나 가짜로 보이는 이메일이 존재하는 경우 또한 고려해야 한다.
Faithfulness가 위반된 몇 가지 예시를 살펴보자.
Truncated data
과거 MS 사의 엑셀은 65,536개의 열과 255개의 행만 사용할 수 있었다. 따라서 데이터 정보가 잘리는 경우가 존재하였다.
Spelling Errors
철자 오류가 발생한 경우이다.
Time Zone Inconsistencies
시간대가 불일치 하는 경우, 동일한 시간대(UTC)를 사용하도록 바꿔줄 수 있다.
Duplicated Records or Fields
중복된 데이터를 제거하고, primary key를 사용하여 식별되게 만들어준다.
Units not specified or consistent
단위가 지정되지 않았거나 일관성이 없는 경우, 단위를 추정하거나 해당 값이 합리적인 범위 내에 존재하는 값인지 확인한다.
Missing data
레코드에 데이터가 아예 존재하지 않는 경우가 존재한다. 이때, 존재하지 않는 데이터는 " ", 0, -1, 999, 12345, 1970, 1900, NaN(Not a Number), Null으로 표기될 수 있다.
이때, 이 missing value의 경우 처리할 수 있는 방법은 아래와 같다.
1. 개수가 많지 않을 때, 아예 날려버려도 전체적인 분석에 영향이 없다면 아예 레코드 전체를 삭제시켜버릴 수 있다.
2. missing value를 NaN으로 설정한 후, 그냥 분석을 진행할 수도 있다.
3. Imputation(대치)이나 interpolation(보간)을 이용하여 missing value에 대해 대략적으로 값을 예측하여 값을 채워넣을 수도 있다.
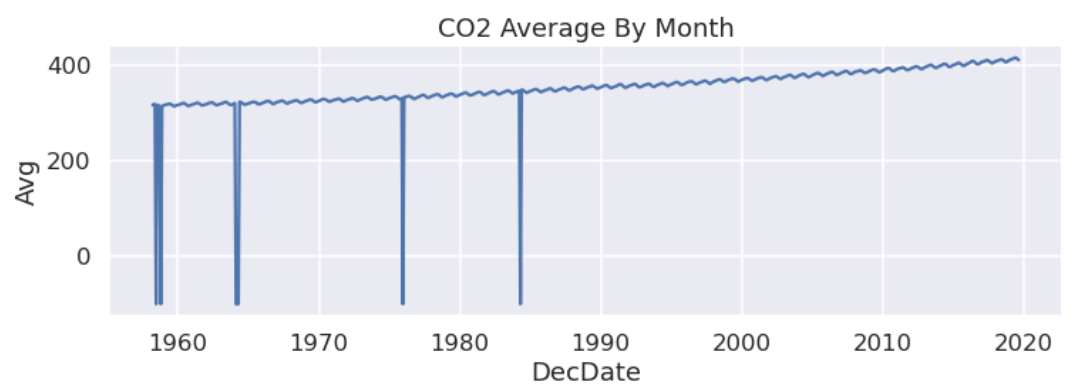
위 사진은 실제로 CO2 배출량에 대한 데이터로 중간중간 Drop된 값이 존재함을 확인할 수 있다.

이때, 위 사진과 같은 방법을 사용할 수 있다.
1번의 경우 missing된 값을 drop시키거나, 2번처럼 missing된 값을 아예 비워버릴 수도 있고, 3번처럼 앞뒤 값의 중간값으로 interpolate할 수도 있다.

위 예시의 경우 누락된 값이 몇 개 없기 때문에 어떤 방법을 사용해도 괜찮지만, EDA를 기반으로 3번 옵션을 선택한 모습을 볼 수 있다.
즉, EDA/Data Wrangling(데이터 전처리) 과정에서 데이터와 메타 데이터를 확인해야 하고, 각 필드와 속성, 차원을 개별적으로 살펴봐야 하는데, 이때 차원 간의 관계 또한 확인해야 한다.
이러한 과정에서 데이터를 실제로 visualization을 진행해 본다던가, 가정이 필요하다면 각 가정이 유효한지 확인해야 한다. 또한 이상 징후(anomalies)를 식별하고 해결해야 하며, 필요에 따라 데이터 correction을 진행해준다.
중요한 점은 데이터를 preprocessing하는 과정을 잘 기록해두는 것이다. 이때 jupyter notebook과 같은 환경을 사용하면, 내가 진행한 데이터 preprocessing 과정이 잘 기록되기 때문에 이러한 툴을 사용하는 것을 추천한다.
이때 preprocessing을 기록하는 것이 중요한 이유를 예로 들자면, 어떤 모델 A를 어떤 데이터를 전처리하여 학습시켰다고 했을 때, 이후 모델을 평가할 때, 앞서 학습 시킨 데이터와 동일한 전처리 과정을 거쳐야 한다. 그런데, 이 전처리 과정을 기록해놓지 않았다면 해당 모델을 돌릴 때 원하는 성능이 나오지 않을 수 있다.
Data Cleaning
data cleaning은 아래와 같은 task로 구성되어 있다.
- 앞서 Faithfulness에서 언급하였던 missing 값 채우기
- outlier나 noise 데이터를 식별하고, smoothing
- 일치하지 않는 데이터 수정
- 여러 곳에 존재하는 데이터를 합쳐 중복을 없애며 redundancy를 줄임
이때 우리가 가장 먼저 살펴 볼 것은 outlier와 noise 처리 방법이다. 이때 우리는 outlier를 중요하지 않은 데이터라고 판단하여 이를 버린다는 가정을 포함하고 있다.
data cleaning의 방법 별로 알아보자.
Binning method
주어진 데이터를 묶어서 생각하는 방법이다. 이때, 각 bin을 최대한 비슷한 사이즈로 채워서 넣는 것이다. 그러면 해당 bin의 평균값, 중앙값과 경계를 통해 smoothing를 진행할 수 있다. 예시를 통해 알아보자.
달러로 표기된 어떤 가격 데이터가 있다고 가정하자. (이 데이터는 sorting된 상태이다.)
4, 8, 9, 15, 21, 21, 24, 25, 26, 28, 29, 34
데이터를 bin으로 나눠줄 때 동일한 크기로 나눠준다.
bin1: 4, 8, 9, 15
bin2: 21, 21, 24, 25
bin3: 26, 28, 29, 34
이제 각 bin에 존재하는 값을 smoothing 해보자.
bin의 평균값(means)을 통해 smoothing을 진행하는 경우이다.
bin1: 9, 9, 9, 9
bin2: 23, 23, 23, 23
bin3: 29, 29, 29, 29
bin의 경계값(boundaries)을 이용하여 smoothing을 진행하는 경우이다. 이 경우 각 bin의 최대값과 최소값을 파악하여, 각 데이터에 대해 더 가까운 쪽으로 smoothing을 진행할 수 있다. 이 방법을 사용하는 경우 means값을 이용한 smoothing 방식에 비해 더 soft하다는 특징이 있다.
bin1: 4, 4, 4, 15
bin2: 21, 21, 25, 25
bin3: 26, 26, 26, 34
Regression

regression 방법의 경우 데이터에 대한 regression을 그린 다음, 해당 linear line으로부터 멀리 떨어진 데이터를 찾아 outlier로 판단한 후 해당 값을 날릴 수 있다.
Clustering

clustering의 경우 데이터를 사진과 같이 표시해 준 후 비슷한 위치에 있는 데이터끼리 cluster를 만들어준다. 이후 각 cluster에 포함되지 않는 값을 이상치로 판단하여 날려줄 수 있다.
다양한 removal method로는 아래와 같다.
- Clustering
- Curve-fitting
- Hypothesis-testing with a given model
- Draw boxplot(통계적 수치 이용)
Combined computer and human inspection
사람이 봤을 때에 이상한 값이나 의심스러운 값을 처리하는 방법이다.
Data discrepancy detection
Data discrepancy은 데이터의 불일치성으로, data cleaning 작업 자체를 하나의 프로세스로 만들 수 있는 과정이다.
메타데이터를 사용하고, 여러 가지 룰에 의해 우리가 이러한 데이터의 불일치성을 확인할 수 있다.
Uniqueness rule (독창적인 규칙)
고유해야 하는 값은 해당 속성의 모든 다른 값과 달라야 한다는 규칙이다.
Consecutive rule (연속적인 규칙)
어떤 속성의 최대값과 최소값 사이에 모든 값이 그 사이에 존재해야 한다는 규칙이다.
Null rule
존재하지 않는 값에 대해 처리하는 방법으로 보통 NaN이나 null로 표시한다.
이때, 추가적으로 필요하다면 commercial(상용화)한 도구를 사용할 수 있다. 우편 번호나, 맞춤법을 검사할 수 있는 도구를 통해 오류를 감지하고 수정하는 Data scrubbing, 규칙이나 관계를 발견하기 위해 이상치를 탐지하는 Data auditing이 있다.
Data Integration
Data Integration는 여러 곳에 포진해있는 데이터를 합치는 과정이다.
- schema integration (스키마 통합)
A.cust-id와 B.cust-#가 어떻게 연결되어 있는지.
- entity indentification problem
동일한 값 없애기
- Detecting and resolving data value conflict
겉으로는 달라보이지만, 사실 동일한 데이터인 경우 충돌할 수 있다. ex) 미터와 마일로 표시되어 있는 거리.
Handling Redundancy in Data Integration
동일한 데이터가 있는 경우 다루는 방법에 대해 알아보자. 이때, 동일한 데이터가 있는 경우를 판단하는 방법이 있다.
1. 일반적으로 눈으로 봤을 때 동일해보이는 정보
2. 달라보이지만 실제로 동일한 정보
따라서 우리는 각 속성에 대해 correlation analysis를 진행하여 실제로 같은 값인지를 확인할 수 있고, 동일하다고 판단되는 값 중 하나를 선택하여 데이터 분석에 사용할 수 있다.
Correlation analysis
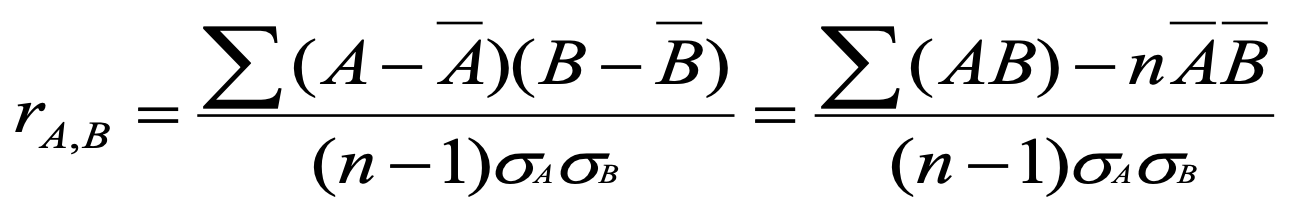
Pearson’s product moment coefficient라고도 불리며, numerical(숫자)한 데이터에 대해 상관관계를 구할 수 있다. 이때, r(A,B)의 값이 양수이면 양의 상관관계를 가지고, 0인 경우 independent 하다고 할 수 있으며, 음수인 경우 음의 상관관계를 가진다고 할 수 있다.
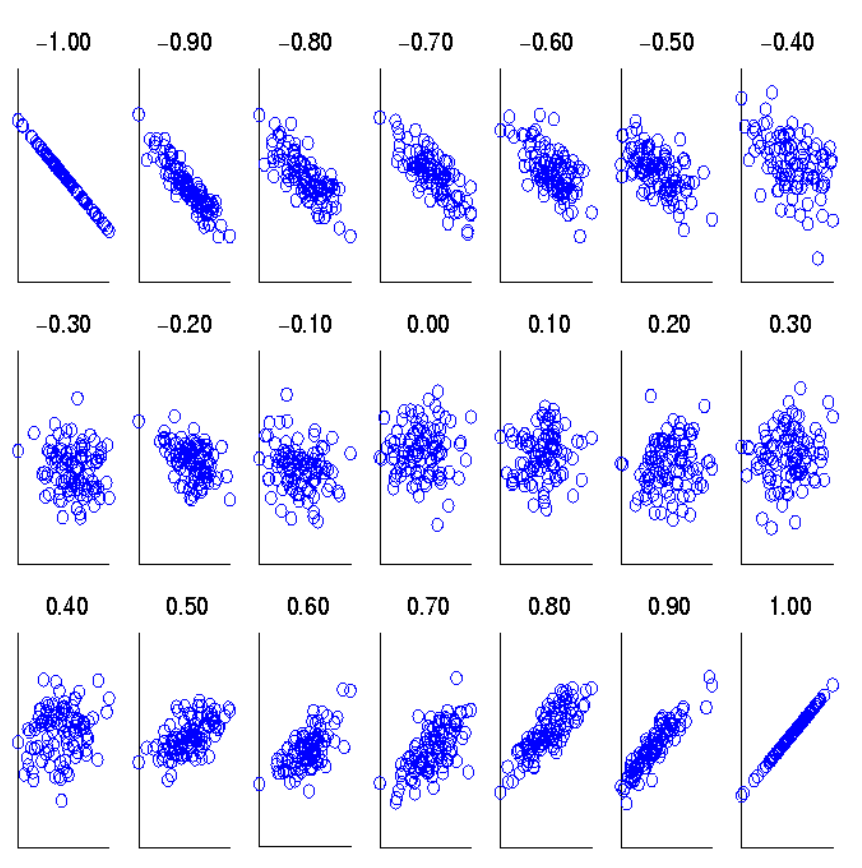
위 사진은 r(A,B)의 값에 따른 상관 관계를 도식화한 모습이다. 이때, r(A,B)의 값이 1이나 -1인 경우 중복되는 속성이므로 각 속성을 서로 대체해서 사용할 수 있다. r(A,B)이 1이나 -1보다는 작은 값이지만, 나름 강한 상관관계를 가진다면 약간의 오류를 감수하고 속성을 대체하여 사용할 수 있다.
Covariance

공분산을 통해 A와 B가 비례하는지에 대한 여부를 확인할 수 있다. 위와 같은 수식을 통해 나타낼 수 있으며, correlation과 수식적으로 어떤 관계에 있는지 생각해볼 수 있다.
X^2(chi-square) test

앞서 correlation을 구할 때는 numerical한 데이터를 사용하였다. 그러나 chi-square test를 진행할 때에는 각 value가 categorical 해야 한다.
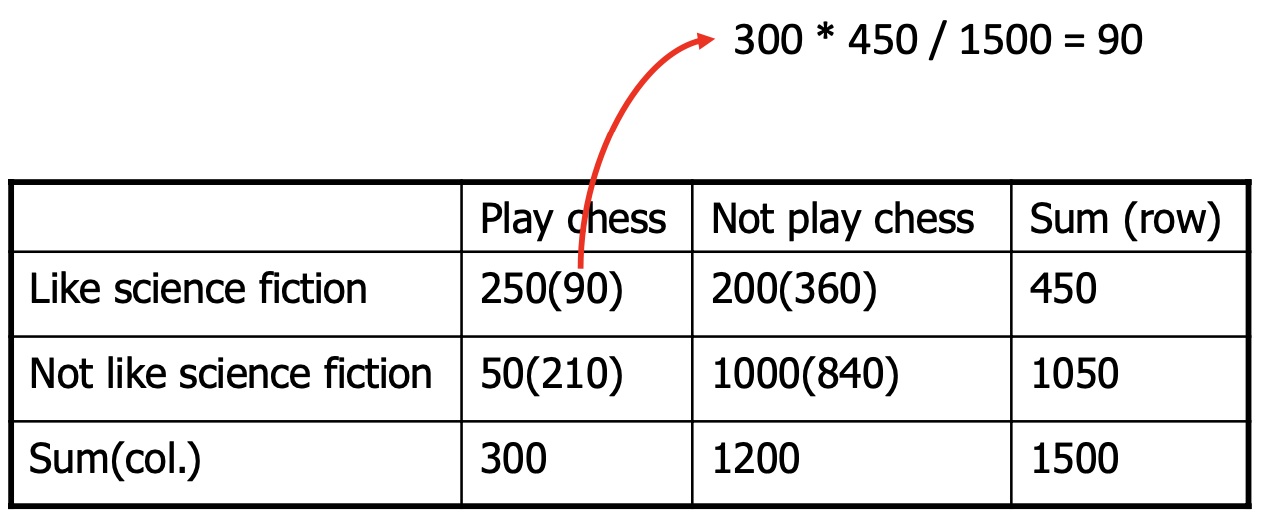
chi-square test의 검증 과정에 대해 알아보자. 위 사진에서 "Like science fiction"를 A라고 하고 "Play chess"를 B라고 했을 때, A와 B 사이에 correaltion이 없는 경우, 즉 독립적이라고 가정했을 때, 위 표의 괄호 안에 있는 값은 expected value이다. 괄호 밖에 있는 숫자는 실제 조사된 값이다.

위 사진은 앞서 제시된 데이터에 대해 x값을 계산한 결과이다. 이때, x의 값이 커질수록 상관관계가 있다. 즉 독립이라고 가정했을 때의 expected value가 실제값과 멀어질 수록 데이터 간의 연관관계가 있다는 의미이다.

위 사진은 chi-square test에 대한 그래프 값이다.
우리는 속성값의 type에 따라 correlation과 coefficient를 계산하거나, X^2(chi-square) test를 진행하여 redundancy를 파악할 수 있다.
Data Transformation
Data Reduction
우리가 가지고 있는 데이터가 large-scale의 데이터인 경우, 해당 데이터를 온전히 다 쓰기에 무리가 있다. 또, 충분한 resource가 없을 수도 있고, 해당 데이터를 이용하여 어떤 결과를 낼 때 시간이 굉장히 오래 걸릴 수도 있다.
따라서 데이터에 대한 속성을 해치지 않으며 빠르게 분석이 가능한 방법을 다루는 부분이 Data Reduction이다. Data Reduction의 방법은 크게 세 가지로 나뉜다.
Dimensionality reduction (차원 축소)
데이터가 가지고 있는 중요하지 않은 attribute를 삭제하는 방법이다. 즉, 각 레코드의 표현을 더 단순화하는 방법이다.
Numerosity reduction (개수 감소)
Data compression (데이터 압축)
데이터 별로 표현 방법을 더 압축시키는 방법이다. 비슷한 예로 파일을 zip으로 압축시킨다거나, 문자열을 압축하는 방법이 있다.
Dimensionality reduction (차원 축소)

데이터의 차원이 높을수록, 처리할 때의 cost가 많이 필요하다. 따라서 demensional reduction을 진행해야 한다. reduction을 진행하면, 관련 없는 feature를 지워줄 수 있기 때문에 noise의 수가 줄고, 데이터 마이닝의 시간 소요가 적다. 또, visualization이 쉬워진다.
차원을 축소하는 방법은 아래와 같다.
Wavelet transforms
신호를 서로 다른 주파수(different frequency subband)로 분해하고, 이 과정에서 덜 중요한 부분을 없앰으로써 데이터에 대한 dimensionaluty에 대한 reduction을 수행할 수 있다.
이때, 우리는 Decrete Wavelet Transform(DWT)는 선형 신호 처리와 다중 해상도 분석을 위해 사용되며, 신호를 다양한 주파수의 subband로 분해한다. 이때, 중요한 wavelet 계수만 저장함으로써 데이터를 압축시킬 수 있는데, 이를 Compressed approximation(압축된 근사)라고 한다.
DWT는 이산 푸리에 변환과 유사하지만, 손실 압축(lossy compression)에서 더 나은 성능을 보이고 공간에 국한된(localized in space) 특성을 가진다.
DWT의 적용방법은 아래와 같다.
1. 변환할 데이터의 길이 L은 2의 제곱수여야 하고, 필요한 경우 0의 padding를 둔다.
2. 이때, smoothing하는 함수와 차이를 구하는(difference) 함수 두 가지를 사용할 수 있다.
3. 데이터의 앞에서부터 2개씩 pair를 맺어 결과적으로 길이가 L/2인 데이터 셋을 생성한다.
4. 2번의 함수를 원하는 길이에 도달할 때까지 재귀적으로 적용한다.
Harr Wavelet
Harr Wavelet를 통해 간단한 예시를 들어보자.
데이터가 S = [2, 2, 0, 2, 3, 5, 4, 4]가 있다고 가정했을 때, Harr Wavelet로 decomposition을 진행하는 방법은 아래와 같다.

위 사진에서 보이는 것처럼 데이터에 존재하는 요소를 2개씩 묶은 후 각각의 평균값을 구해 압축을 진행한다. 이때, 길이가 1이 될 때까지 압축을 진행시켜준다. 오른쪽에 존재하는 Detail Coefficients는 각 압축된 값을 복원하기 위해 존재하는 값이다.
위 사진의 보라색과 분홍색 글씨처럼, 결과로 나온 값에 detail coefficient를 더하면 앞의 값, 빼면 뒤의 값이 나오기 때문에 이를 통해 데이터를 원상복구 시킬 수 있다. 결과값을 저장할 때에는 평균의 마지막 element와 이어지는 coefficient를 역순으로 저장하면 된다.
즉, Harr Wavelet의 결과값은 SA = [2.75, -1.25, 0.5, 0, 0, -1, -1, 0]으로 이 값 만으로도 원래의 데이터를 가져올 수 있다.
우리가 실제로 reduction을 진행할 때 앞으로 갈수록 전체 시퀀스에 영향을 많이 미치고, 뒤로 갈수록 영향이 작아진다. (위 결과에서도 마찬가지로 앞에 존재하는 데이터일수록 전체 숫자에 영향을 많이 끼친다.) 따라서 결과값에서 푸른색에서 붉은색으로 갈수록 unnessary하다고 할 수 있다.

위 트리는 앞선 Harr Wavelet의 결과값에 존재하는 coefficient가 원래 벡터에 영향을 미치는 위치를 나타낸 트리 구조이다. 첫 번째 값은 당연히 데이터 전체에 영향을 미치며, 두 번째 coefficient부터 +, -에 따라 영향을 미치는 벡터의 위치가 변화하고 있음을 알 수 있다.
Wavelet transform의 특징은 아래와 같다.
- 값 자체가 cluster되는 모양을 볼 수 있으며, hat 모양을 통해 해당 정보의 중요도를 나열해준다.
- 중요한 정보를 수집하고자 하는 특성으로 인해 자연스럽게 outlier를 제거할 수 있다.
- 여러 해상도(resolution)를 표현할 수 있기 때문에 정확도나 smoothing 정도를 결정할 수 있다.
- O(N)의 효율적인 시간 복잡도를 가지고 있다.
- 저차원의 데이터에만 적용이 가능하다.
Principal Component Analysis (PCA)
Numerosity reduction (개수 감소)
Parametric method
Regression analysis
Non-parametric method
Histogram analysis
Clustering
Sampling
Data Compression (데이터 압축)
Data Discretization (데이터 이산화)
우리는 여러 interval(간격) 중에 countinuous한 value가 존재하는 경우 각 값을 discrete한 interval로 표현할 수 있다. 이때, 이산화하는 method는 Binning, Histogram analysis, Correlation, Clustering, Decision-tree analysis가 있다.

위 사진은 클래스 label을 사용하지 않은 이산화 그래프로 binning과 clustering 방법을 사용하여 나타낸 모습이다.
Discretization by Classification & Correlation Analysis
Classification
Classification의 경우 그다지 적합하지는 한다. Decision Tree는 주어진 데이터를 계층적으로 구분하는 방법으로 각 노드의 값은 나눠진 데이터의 대표값이라고 할 수 있다.
Correlation Analysis
Concept Hierarchy Generation
'Computer Science > 데이터 과학(Data Science)' 카테고리의 다른 글
| [데과/DS] Feature Engineering (0) | 2024.04.30 |
|---|---|
| [데과/DS] Visualization Theory (0) | 2024.04.29 |
| [데과/DS] Data Understanding & Visualization (0) | 2024.04.29 |
| [데과/DS] Regular Expression (정규 표현식) (1) | 2024.04.28 |
| [데과/DS] Data Acquisition (데이터 취득) (0) | 2024.04.28 |