Data Understanding
데이터를 모델링하기 전 데이터의 퀄리티 관점에서 충분한지 판단을 해야 한다. 판단 기준은 아래와 같다.
Conpleteness
수집된 데이터의 크기나 범위를 말한다.
Data Visualization
Distribution
각 변수가 어떤 frequency로 나타나는지를 표현하는 것을 distribution이라고 한다. 이때 모든 값이 나올 빈도를 모두 더했을 때 100%가 되어야 하며, 우리가 관찰하는 데이터의 수와 같아야 한다.

위 데이터가 분포를 잘 보여주고 있는가라고 묻는다면 답은 아니오이다. 위 차트는 60대 이상의 사람을 대상으로 10년 전과 비교하여 여가 시간의 변화량 보여주고 있다. 이때, 위와 같은 차트는 하나의 개인이 여러 개의 카테고리에 속할 수 있을 뿐만 아니라, 각 값을 모두 합쳤을 때, 100이 되지 않기 때문이다.

위 데이터도 마찬가지로 분포를 잘 설명하지 못하고 있다. 위 차트는 10대들이 SNS에 올리는 글의 주제에 관해 보여주고 있다. 이때도 마찬가지로, 개인이 여러 개의 범주에 속해 있을 수 있으며, 모든 값의 합이 100이 되지 않기 때문에 위 차트는 분포를 나타내고 있다고 할 수 없다.

위 사진의 경우 분포를 나타내고 있다. 위 차트는 소득 계층에 대한 분포를 보여주는 차트로 각 개인은 정확히 하나의 범주에 속하며, 우리가 보는 값은 해당 범주에 속하는 개인의 비율이기 때문이다.
다양한 정보를 시각화할 때 사용하는 방법에 대해 알아보자.
Simple Table

Simple Table은 Value Table이라고 하며, 사진과 같이 단순하게 값을 나열한 것이다. 그러나 직관적으로 이해하기 어렵기 때문에 속성을 한눈에 파악하기에 어려움이 있다.
그러나 simple table의 경우 논문에서 자주 등장한다. 보통 데이터 셋의 사이즈나 평균과 같은 단편적인 대표값을 보여줄 때 유용하기 때문이다. 또, 위 사진과 같이 제안한 방법들에 대한 성능을 비교할 때에도 사용하기 좋다.
import pandas as pd
"""
source: https://heartbeat.comet.ml/exploratory-data-analysis-eda-for-categorical-data-
870b37a79b65
"""
def frequency_table(data:pd.DataFrame, col:str, column:str):
freq_table = pd.crosstab(index=data[col],
columns=data[column],
margins=True)
rel_table = round(freq_table/freq_table.loc["All"], 2)
return freq_table, rel_table
buying_freq, buying_rel = frequency_table(car_data, "class", "buying")
print("Two-way frequency table")
print(buying_freq)
print("---" * 15)
print("Two-way relative frequency table")
print(buying_rel)
코드는 위와 같이 작성할 수 있다.
Bar Plot

위 사진과 같이 카테고리 별로 frequency가 어떤지 보여줄 때 위 사진과 같이 막대 형식으로 나타낸 모습을 Bar Plot이라고 한다.
"""
Starter code from tutorials point
see: https://bit.ly/3x9Z6HU
"""
import matplotlib.pyplot as plt
# Dataset creation.
programming_languages = ['C', 'C++', 'Java', 'Python', 'PHP', "Other", "None"]
employees_frequency = [23, 17, 35, 29, 12, 5, 38]
# Bar graph creation.
fig, ax = plt.subplots(figsize=(10, 5))
plt.bar(programming_languages, employees_frequency)
plt.title("The number of employees competent in a programming langauge")
plt.xlabel("Programming languages")
plt.ylabel("Frequency")
plt.show()
코드는 위와 같이 작성할 수 있다.
따라서 bar plot은 기본적으로 단순히 숫자를 보여주며 frequency를 보여주기 좋다.

그러나 bar plot를 통해 데이터를 시각화할 때 스케일을 잘 설정해서 보여줘야 한다. 예를 들어 A 카테고리의 값이 100만 단위인데, B 카테고리의 값이 10의 단위일 때 bar plot을 그리면, B 카테고리의 값이 거의 0에 가깝게 보이기 때문이다. 따라서 작은 값에 대한 비교가 어렵다.
따라서 우리가 데이터를 그래프로 그릴 때 각 값에 대해 log를 취해주는 등의 스케일을 선택할 수 있다.
Pie Charts

pie charts는 distribution을 보여줄 때 효과적이며, 보통은 데이터가 balanced한지, imbalanced한지를 판단하기 위해 주로 사용된다.
또, 만약 데이터가 imbalance하다면 각 카테고리 별로 major한 것이 어떤 것인지, 얼마나 많이 차지하고 있는 것인지를 보여줄 수 있다. 하지만, 표현해야 할 카테고리의 개수가 많아지면 가독성이 낮아진다는 단점이 존재한다.
"""
Example to demonstrate how a pie chart can be used to represent the market
share for smartphones.
Note: These are not real figures. They were created for demonstration purposes.
"""
import numpy as np
from matplotlib import pyplot as plt
# Dataset creation.
smartphones = ["Apple", "Samsung", "Huawei", "Google", "Other"]
market_share = [50, 30, 5, 12, 2]
# Pie chart creation
fig, ax = plt.subplots(figsize=(10, 6))
plt.pie(market_share,
labels = smartphones,
autopct='%1.2f%%')
plt.title("Smartphone Marketshare for April 2021 - April 2022",
fontsize=14)
plt.show()코드는 위와 같다.
Line Graphs and Area Charts

위 그래프는 기간 별 팔린 운동화의 개수를 simple line graph로 나타낸 모습이다.
import matplotlib.pyplot as plt
# Data creation.
sneakers_sold = [10, 12, 8, 7, 7, 10]
dates = ["Jul '1", "Jul '7", "Jul '14", "Jul '21", "Jul '28", "Jul '31"]
# Line graph creation
fig, ax = plt.subplots(figsize=(10, 6))
plt.plot(dates, sneakers_sold)
plt.title("Sneakers sold in Jul")
plt.ylim(0, 15) # Change the range of y-axis.
plt.xlabel("Dates")
plt.ylabel("Number of sales")
plt.show()코드는 위와 같이 작성할 수 있다.

이때 위 사진과 같이 Area Charts로 표현하면 효과적이며, 전체에 대한 area가 표시된다. 오른쪽과 같이 운동화의 브랜드 별로 그래프를 나타낼 수도 있다.
# Area chart creation
fig, ax = plt.subplots(figsize=(10, 6))
plt.fill_between(dates, sneakers_sold)
plt.title("Sneakers sold in Jul")
plt.ylim(0, 15) # Change the range of y-axis.
plt.xlabel("Dates")
plt.ylabel("Number of sales")
plt.show()코드는 위와 같다.
Scatter Plots

scatter plot의 경우 각 데이터 포인트를 해당되는 위치에 하나씩 찍어준다. 이때, 오른쪽 그래프처럼 카테고리 별로 색을 다르게 하여 점을 찍어줄 수 있고, 왼쪽 그래프처럼 어떤 데이터에 대해 regression line, 즉 fitting line을 그려 데이터가 선형적인 관계가 있음을 나타낼 수도 있다.
그러나 fitting line을 그릴 때, linear line으로 나타날 수 없는 데이터의 경우 아무리 best fit한 linear line을 찾아도 해당 데이터를 잘 표현할 수 없다. 즉, 해당 데이터가 선형 관계를 가지고 있지 않은데 선형 수식으로 나타내려고 하는 경우 주의해야 한다.
반대로 선형 관계인데, 엉뚱한 linear line을 그려놓고 선형적이지 않다고 판단할 수 있다. 따라서 scatter plot은 해당 데이터가 선형 관계에 있으니 그 점을 고려하라는 일종의 의도가 들어가는 visualization이라고 할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
# Data creation.
temperature = np.array([30, 21, 19, 25, 28, 28]) # Degree's celsius
ice_cream_sales = np.array([482, 393, 370, 402, 412, 450])
# Calculate the line of best fit
X_reshape = temperature.reshape(temperature.shape[0], 1)
X_reshape = np.append(X_reshape, np.ones((temperature.shape[0], 1)), axis=1)
y_reshaped = ice_cream_sales.reshape(ice_cream_sales.shape[0], 1)
theta = np.linalg.inv(X_reshape.T.dot(X_reshape)).dot(X_reshape.T).dot(y_reshaped)
best_fit = X_reshape.dot(theta)
# Create and plot scatter chart
fig, ax = plt.subplots(figsize=(10, 6))
plt.scatter(temperature, ice_cream_sales)
plt.plot(temperature, best_fit, color="red")
plt.title("The impact of weather on ice cream sales")
plt.xlabel("Temperature (Celsius)")
plt.ylabel("Ice cream sales")
plt.show()코드는 위와 같다. 위 코드에서 numpy의 reshape() 함수를 통해서 y 절편을 계산하는 등의 과정을 거쳐, 각 포인트에 대해 직선 거리의 합이 최소가 되는 best fit line을 찾을 수 있다.
Heatmaps

많은 숫자 값을 일반화시켜 보여준다.
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
data = np.random.rand(8, 10) # Graph will change with each run
fig, ax = plt.subplots(figsize=(10, 6))
sns.heatmap(data)
plt.title("Random Uniform Data")
plt.show()코드는 위와 같다.
Treemap
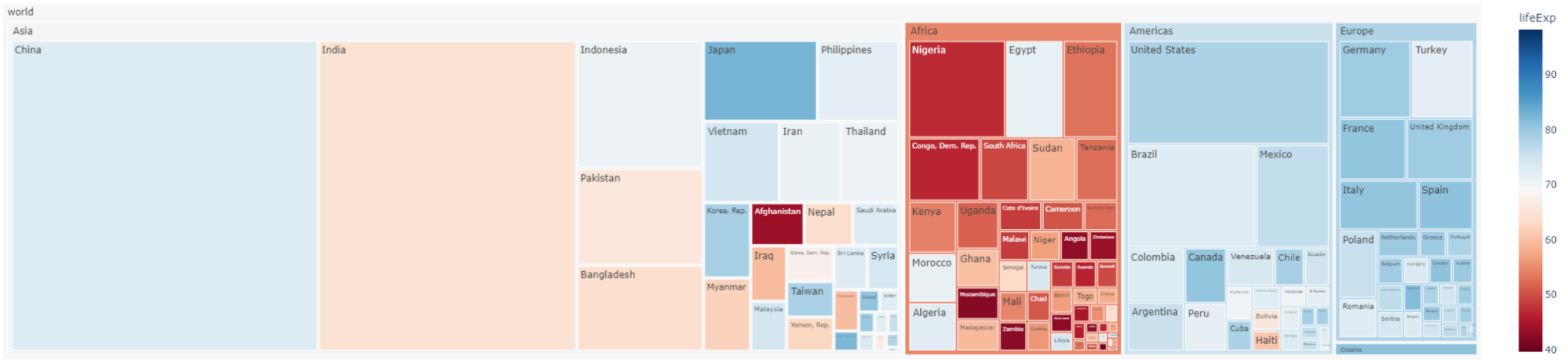
treemap는 데이터가 hierarchically하게 분포되어 있는 경우 해당 계층 구조를 잘 나타낼 수 있다. 위 사진은 world, Asia, Afreeca, China 등으로 데이터가 구성되어 있다. 이때 색상을 통해 각 면적이 해당 카테고리의 규모가 됨을 알 수 있다.
그러나 논문과 같은 자료의 경우 treemap을 잘 사용하지 않는데, 왜냐하면 위와 같이 그래프를 그릴 경우에 논문에 첨부하게 되면 글씨가 굉장히 작아져 읽는 데에 문제가 있을 수 있기 때문이다.
Example Dataset
Histograms
Evaluating Histograms
Box and whisker plot
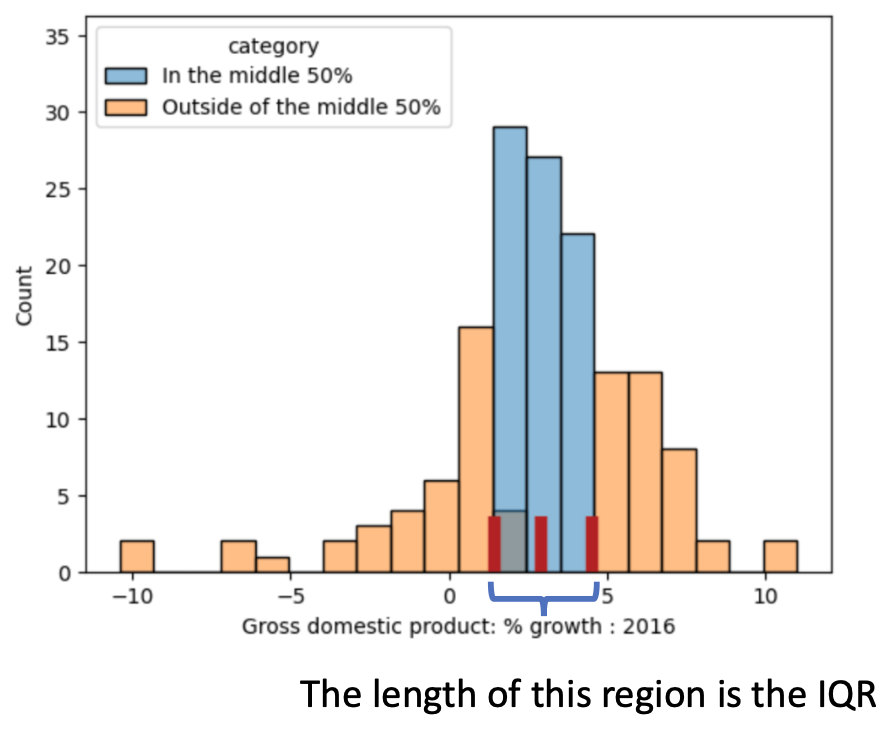
outlier를 정하는 방식에 대해 알아보자. 우리는 outlier를 정의할 때 box plot을 사용할 수 있다. 몇 가지 키워드를 알아보자.
- first or lower quartile: 25th percentile
- second quartile: 50th percentile (중간값)
- third or upper quartile: 75th percentile
이때, first quartile과 third quartile 사이에는 전체 데이터의 50%가 들어간다고 해서, 그 사이를 Interquartile range(IQR)라고 부른다. 즉, IQR = third quartile – first quartile
우리는 이러한 IQR을 기반으로 box plot를 그릴 수 있다.
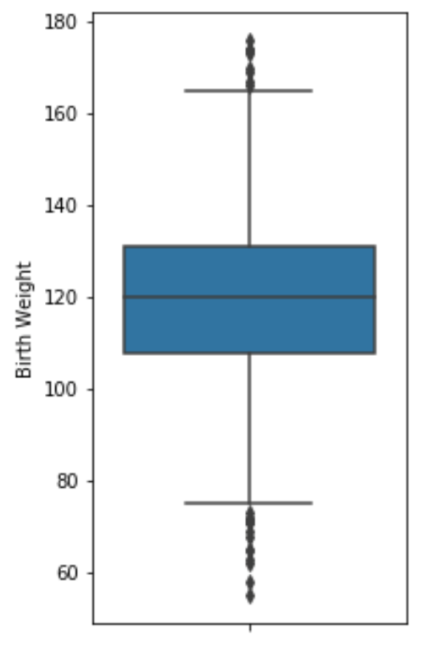
box plot는 numerical distribution(수치 분포)의 여러 특성을 요약한다. 또한, Lower quartile, Median, Upper quartile과 IQR을 기반으로 하여 그림의 위 아래에 존재하는 선(whisker)을 그리고, 해당 선에 대해 outlier를 표현할 수 있다.
이때, 각 whisker은 수염으로 보통 lower quartile에 1.5*IQR을 뺀 값과, upper quartile에 1.5*IQR을 더한 값으로 설정하며, 해당 선 밖에 있는 데이터를 outlier라고 정의할 수 있다. 이때 1.5라는 수는 통계학적으로 정의된 수이다. 이때, 데이터를 더 정확히 나타내고 싶다면 관습적으로는 1.5를 사용하지만 때에 따라 2배인 3을 사용한다고 한다.
해당 distribution이 normal 분포를 따를 때, 위쪽 whisker line과 아래쪽 whisker line 사이에 들어가는 데이터는 99.3% 정도 된다고 한다.

box plot의 각 위치를 각 값에 대응시킨 사진이다.
Violin plots
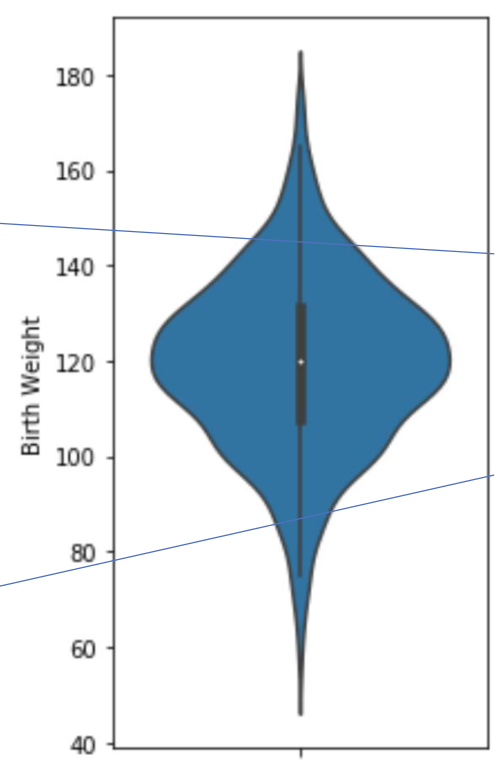
violin plot의 경우 box plot와 비슷한 모습을 띄는데, 이때 위 사진에서 흰색 점은 median을 의미한다.

이 부분을 통해 third quartile과 first quartile을 확인할 수 있으며, 전체 plot에서 중앙의 세로선이 끊긴 곳을 기준으로 outlier를 정의할 수 있다. 이때, violin plot의 경우 dense 정보가 추가적으로 들어가며, curve의 형태로 density(조밀도)를 판단할 수 있다.
Comparing Distributions
Kernel Density Estimate
Smoothing in 1D

1차원에서 데이터를 smoothing하는 과정이다. 이때, Rug plot의 경우 데이터 포인트를 직접 선으로 그은 모습이다. 따라서 각 데이터가 dense하게 모여있으면 그 부분에 데이터의 분포가 높다고 판단할 수 있다.
이러한 데이터를 조금 더 smoothe하게 표현하면 가운데의 histogram으로 나타낼 수 있다. 따라서 데이터가 더 distribution으로 이해가 된다.
histogram에서 조금 더 continuous하게 그리면 Kernel Density Estimate(KDE)가 된다. 결국 KDE는 probabilty density function, 즉 확률 밀도 함수를 estimation(추정)하는 것이다.
Kernel Density Estimate

앞서 우리는 KDE가 데이터 셋의 확률 밀도 함수를 추정하는 데에 사용된다고 언급하였다. 이때, 그래프로 그려지는 밀도 곡선의 면적은 1이 되어야 한다. 확률 밀도 함수의 특징이기 때문이다.
KDE를 생성하는 과정은 아래와 같다.
1. 각 데이터 포인트에 커널 함수를 놓는다.
2. 커널 함수를 정규화하여 총 면적이 1이 되도록 한다.
3. 모든 커널 함수를 합친다.
각 과정을 자세히 살펴보자.
1. Place kernels
우리는 1단계를 수행하기 전, 어떤 커널 함수를 사용할지 결정해야 한다. 또한 해당 커널 함수의 smoothing parameter도 설정해야 한다. 이 예시에서 우리는 가우시간 커널 함수를 사용하고, 여기에 필요한 smoothing parameter은 alpha로 1의 값을 사용한다.
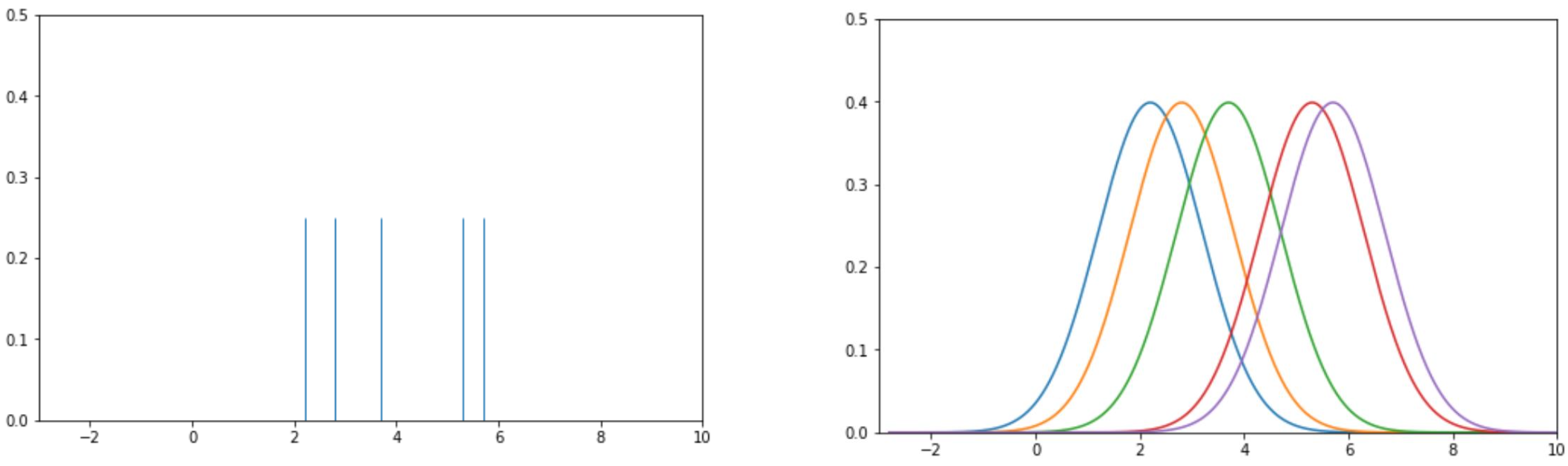
가장 먼저 오른쪽 사진처럼 5개의 데이터에 대해 rug plot를 그린다. 이후 각 데이터에 대해 가우시안 커널 함수를 적용하여 오른쪽과 같이 가우시안 커널을 그려준다. 이때의 alpha는 1이다.
2. Nomalize Kernels
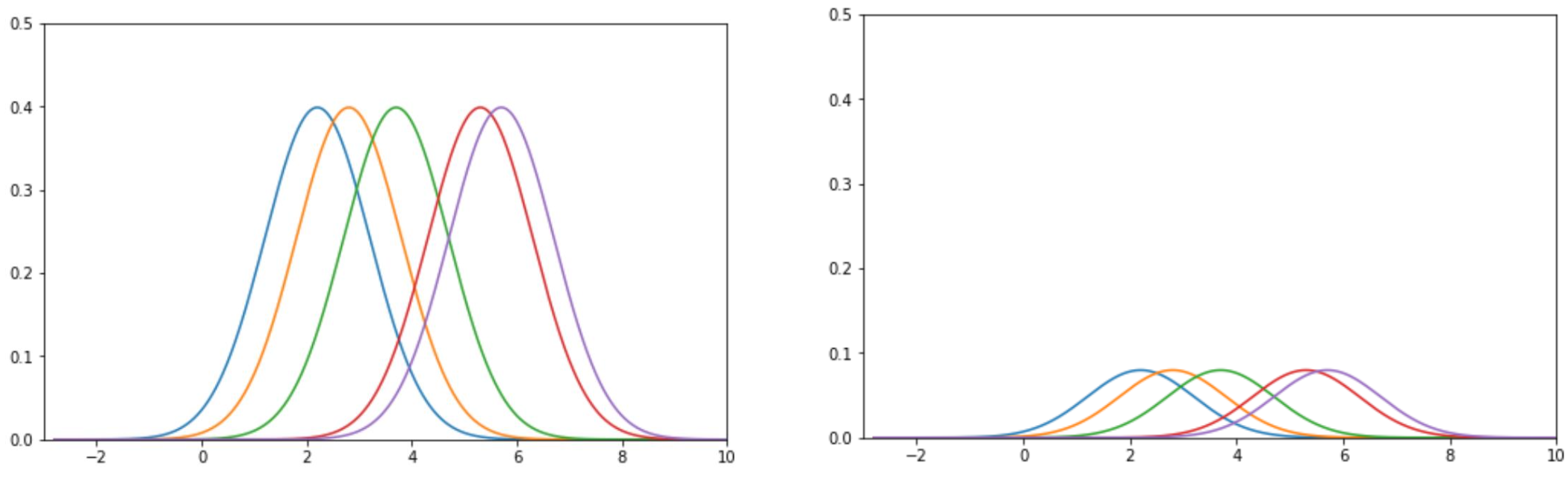
우리는 나중에 이러한 각 커널의 값을 합해야 하기 때문에 정규화를 진행해야 한다. 그런데 각 데이터 값의 대한 가우시안 커널은 각 1의 면적을 갖기 때문에, 모든 경우에 대해 1/5을 곱해주어 정규화를 진행해줄 수 있다.
3. Sum Normalized Kernels

각 값을 모두 더해줌으로써 sns.displot로 생성한 KDE 그래프와 모습이 동일한 그래프를 만들어 낼 수 있다.
이러한 KDE 아이디어 자체는 관찰된 데이터 포인트에 대해 앞으로 등장할 데이터도 해당 포인트 근처에서 등장할 확률이 높아지기 때문에, 해당 데이터 포인트를 기준으로 kernel function을 그릴 수 있다.
위의 과정을 공식화하면 아래와 같다.
1

위 커널 함수는 관측값 i에 중심화된 커널이다. 각 커널은 면적이 1이며, x는 함수의 입력값이다. 가장 자주 사용되는 커널함수는 가우시안 함수이며 식은 아래와 같다.

2
이때, n은 데이터의 총 개수로 KDE의 총 면적이 1이 되기 위해 1/n을 곱해준다.
3
xi는 관측된 데이터 포인트를 말한다. 우리는 여러 개의 커널을 합산하여 KDE를 생성한다.
이때 앞서 언급된 smoothing parameter인 alpha값은 대역폭으로 KDE 생성 시 커널의 폭을 설정할 수 있다. 즉, 데이터 포인트의 영향을 받는 범위를 조정하여 alpha 값이 너무 작은 경우 noise를 생성할 수 있고, 너무 큰 경우 데이터의 특징을 없앨 수 있다.

KDE의 식을 표현하면 위 사진과 같다.
Kernel Functions
커널 함수로는 어떤 것을 사용할 수 있을까? 커널 함수의 조건은 모든 입력에 대해 non-negative, 즉 그 자체로 probabailty density function으로 우리가 활용할 수 있어야 한다. 또한, 그렇기 때문에 적분하면 1의 값이 나와야 한다.
우리가 가장 자주 사용하는 것은 가우시안 커널이며, 식은 아래와 같다.

이때, 파라미터로 알파 값이 들어가는데, 이 알파 값은 KDE의 모양에 대해 smoothness한 정도를 결정해 준다는 것만 인지하면 된다.
bandwidth
위 사진과 같은 히스토그램이 존재한다고 했을 때 bandwidth(대역폭) 파라미터 알파의 값에 따라 KDE에 미치는 영향을 알아보자. 이때, 각 대역폭은 히스토그램의 bin(각 구간)의 넓이에 비유할 수 있다.

위 사진은 알파 값에 따른 KDE의 변화로 알파값이 0.1인 경우 굉장히 울퉁불퉁한 그래프의 모습을 띠고 있다. 반면 알파값이 10인 경우 굉장히 부드럽게 나타나고 있다. 알파값이 10인 경우 굉장히 부드러운 KDE가 나타나는 것은 사실이지만, 너무 부드럽게 표현되는 경우 원래의 데이터 분포와 다른 모양을 띠고 있기 때문에 너무 높은 값을 주는 것도 옳지 않다.
Relationships Between Quantitative Variable
Scatter Plots
Hex Plots
Contour Plots
Generalizing to 2D
'Computer Science > 데이터 과학(Data Science)' 카테고리의 다른 글
| [데과/DS] Data Preprocessing (0) | 2024.04.30 |
|---|---|
| [데과/DS] Visualization Theory (0) | 2024.04.29 |
| [데과/DS] Regular Expression (정규 표현식) (1) | 2024.04.28 |
| [데과/DS] Data Acquisition (데이터 취득) (0) | 2024.04.28 |
| [데과/DS] Data Mining/Science Algorithms (1) | 2024.04.28 |