본 포스트는 2024년 봄 학기 충남대학교 이종률 교수님의 데이터 과학 강의 정리자료입니다.

데이터 마이닝과 데이터 과학 알고리즘은 위 사진과 같이 두 가지의 task로 나눌 수 있다.
Predictive
어떤 입력으로부터 unseen 데이터, 즉 label이 없는 데이터에 대해 예측을 하는 task이다. 기계학습 관점으로는 supervised learning와 가깝다.
Descriptive
데이터를 다른 task에 활용할 수 있도록 데이터가 가지고 있는 속성, struct 또는 semantic 등을 추출하는 task이다. 기계학습 관점으로는 unsupervised learning와 가깝다.
Classification
Clustering
Association Rule Mining
Regression
regression은 classification과 비슷한 방법이다. classidication에게 클래스를 무한의 개수로 갖게 한다면 regression과 동일해지기 때문이다. 결국 regression은 우리가 예측하고자 하는 타겟이 바뀐 것 뿐이다.
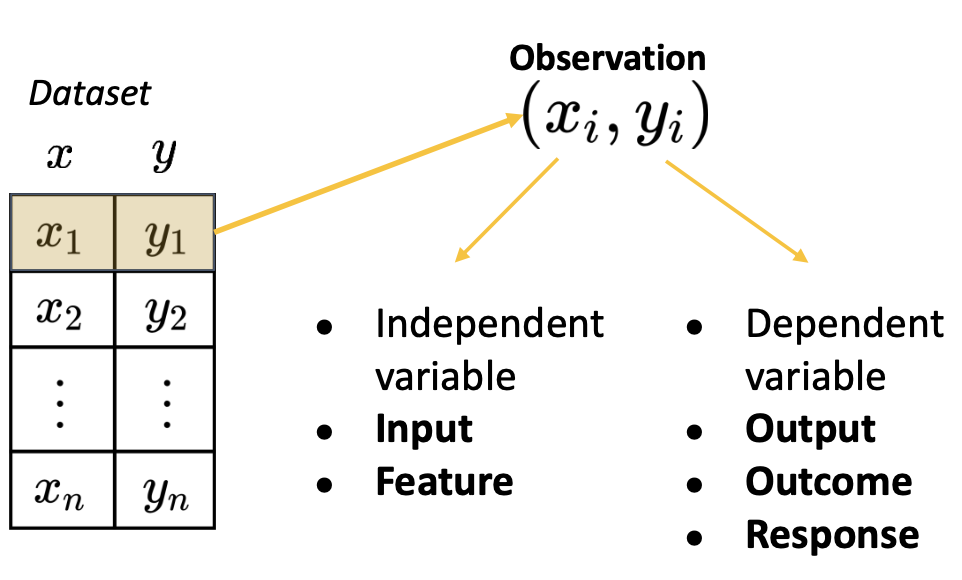
Regression을 formal하게 표현하면 위 사진과 같다. 어떤 데이터셋 x,y가 존재하는데, x는 입력의 feature이며 independent한 값이다. y는 dependent한 값이며 output, outcome, response라고도 한다.

prediction은 x를 활용하여 y를 예측하는 것이다. 그런데, 예측값 y는 실제 결과 y와 다르기 때문에, 둘을 구분하기 위해 예측값에는 hat을 붙여 Ŷ과 같이 나타낼 수 있다.

우리가 예측값 Ŷ를 구하기 위해 어떤 모델을 만들 수 있다. 모델의 생김새는 위 사진과 같으며 θ(세타)는 파라미터, x는 입력값이 된다.
위 사진에서 두 번째 식은 x값이 존재하지 않는데, 이 경우는 입력이 없어도 대략적으로 결과를 에측할 수 있는 경우이다. 예를 들어 어떤 과목이 시험 점수가 매년 50점이었다면, 어떤 과목의 이번 평균도 50점이라고 예측할 수 있는 것처럼 말이다. 그러나 이러한 경우가 흔한 것은 아니다.
parametric model

우리는 parametric model만 다뤄볼 예정이다. 이때 parametric model이란 몇 개의 parameter로 나타낼 수 있는 모델을 이야기하는데, 딥러닝의 경우에는 파라미터의 개수가 굉장히 많기 때문에 "몇 개"라는 명제가 항상 참은 아니다.
전통적인 ML 또는 simpel linear regression의 경우에 해당이 되는 말이며, 이러한 모델은 θ로 표현할 수 있으며, 모델을 fitting하는 과정이 존재한다. 모델을 fitting할 때에는 트레이닝 데이터로부터 우리가 원하는 best θ값을 구하는 일종의 estimation이라고 할 수 있다.

그리고 우리는 실제 트레이닝 된 결과의 θ 또한 위 사진과 같이 θ^으로 표현할 수 있다. 즉, 우리가 원하는 것은 트레이닝 데이터 셋에 대해 가장 최적의 결과를 낸 θ를 얻는 것이다.
Modeling Process
regression 모델링을 하기 위한 과정은 아래와 같다.
1. Choose a model (모델 정하기)
2. Choose a loss function (loss 함수 정의하기)
3. Fit the modle (모델을 학습시켜 최적의 파라미터를 구하기)
4. Evaluate model performance (모델의 성능 평가하기)
이제 각 과정에 대해 자세히 알아보자.
1. Choose a mode
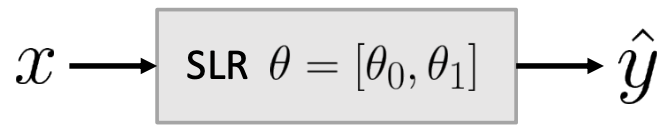
Simple Linear Regression(SLR)은 parametric model이다. 즉, 데이터를 기반으로 하여 입력과 출력 사이의 관계를 가장 잘 표현할 수 있는 θ를 찾는 모델이다.
보통 이러한 입력과 출력 사이의 관계는 non-linear한 경우가 더 많다. 하지만 실질적으로 우리가 가장 이해하기 쉬운 형태는 결국 linear한 형태이고, linear한 모델도 충분히 입력과 출력 사이의 관계를 잘 표현할 수 있기 때문에 자주 사용된다고 한다.
2. Choose a loss function
다음으로는 loss function을 정의해야 한다. 이때, Loss function이란 우리가 예측한 값이 실제 값과 얼마나 떨어져 있는지를 나타내는 metric으로 예측값이 실제값과 가까울 수록 그 값이 작아진다.
일종의 penalty를 준다고도 표현하는데, 이러한 penalty 값을 minimize하는 방향으로 우리는 모델의 최적화를 진행할 수 있다.
이러한 loss function에는 다양한 종류가 존재하는데, loss function을 어떤 task에 적용을 하는지에 따라 영향을 끼치고 loss function에 대한 계산 비용도 존재하기 때문에 우리는 여러 가지 조건에 의해 loss function을 정의할 수 있다.
몇 가지 loss function에 대해 알아보자.
L1 Loss (Absolute Loss)
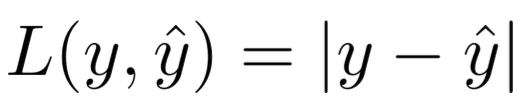
L1 Loss의 경우 절대값을 이용하는 손실함수이다. 즉, 실제 값에서 예측 값을 빼고 그 결과값에 절댓값을 씌운 형태이다.

loss function을 기준으로 y^을 모델로 정의하면 위 사진과 같이 표현할 수 있다.
L2 Loss (Squared Loss)

L2 Loss의 경우 제곱을 이용하는 손실함수이다. 즉, 실제 값에서 예측 값을 뺀 결과값을 제곱하는 형태로 L1 Loss보다 손실에 대해 더 큰 penalty를 가지게 되어 L2 Loss를 더 범용적으로 사용한다.
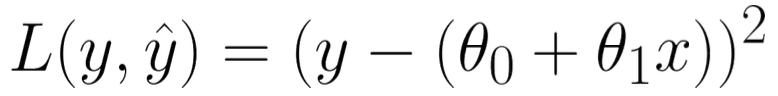
마찬가지로 loss function을 기준으로 y^을 모델로 정의하면 위 사진과 같이 표현할 수 있다.
Average Loss(Empirical Risk)
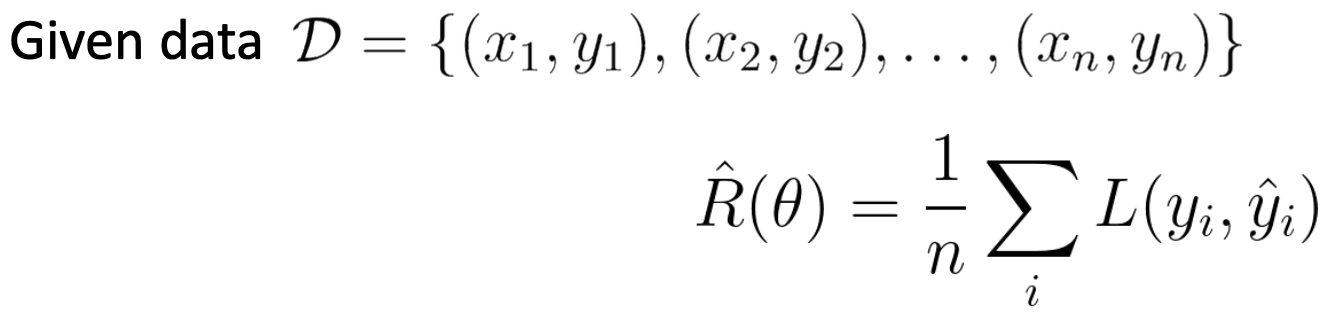
위에서 언급한 L1/L2 Loss의 경우 어떤 한 가지 입력에 대해서 loss를 계산할 수 있는 식이다. 그런데 우리가 가지고 있는 데이터는 굉장히 많기 때문에 모든 데이터에 대한 Loss를 구해 평균으로 만드는 방법을 사용하는데, 이 방법을 Empirical risk 또는 Average Loss라고도 한다.
우리는 이러한 평균값을 최종 loss function으로 사용하게 된다. 결국 Average Loss는 모델이 해당 데이터에 대해 얼마나 fit을 잘하고 있는지를 보여주는 값이라고 할 수 있다. 하지만 트레이닝 데이터와 실제 ditribution은 차이가 있을 수 있기 때문에 Average Loss가 실제 모델의 최종 정확도와 관련이 있는 것은 아니다.

앞서 언급한 L2 Loss를 average loss로 표현하면 위 사진과 같이 Mean Squeared Error로 나타낼 수 있다.

마찬가지로 L1 Loss의 경우 Mean Absolute Error으로 나타낼 수 있다. 이때, 이 MAE도 경우에 따라 자주 쓰이지만, MSE가 가장 자주 사용된다.
3. Fit the modle - Minimizing MSE
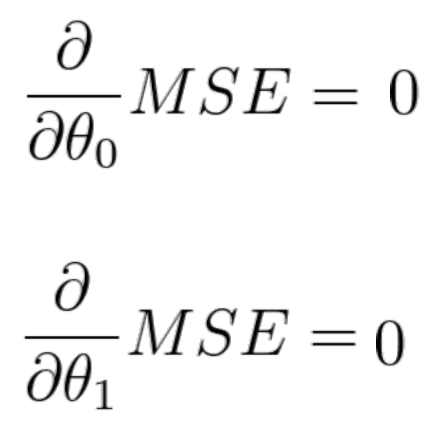
그렇다면 우리는 MSE를 최소화하기 위해 어떤 방법을 사용할 수 있을까? 바로 도함수를 사용하는 것이다. 위 사진과 같이 best 값을 찾기 위해 도함수를 0으로 세팅할 수 있다.
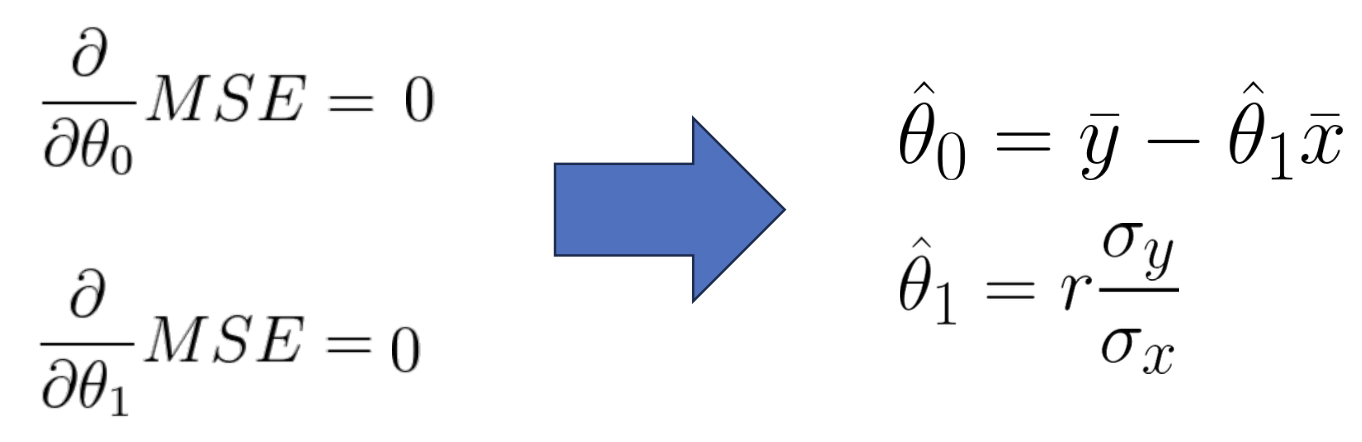
우리는 θ0와 θ1에 대해 위와 같이 값을 구할 수 있다. 그런데, 이 경우와 달리 한 번에 결과값이 나오지 않는 경우도 있는데, 이러한 경우 gradient descent(경사하강법)을 사용하여 최적의 θ를 찾을 수 있다.
4. Evaluate model performance
주어진 트레이닝 데이터를 통해 θ값을 계산하여 최소값일 때의 θ0과 θ1을 찾았다는 것은 loss function을 최소화했다는 의미로 우리가 원하는 모델을 얻은 것이다. 그러면 우리는 모델을 최종적으로 평가해야 한다. 모델을 평가하는 방법은 아래와 같다.
Visualize data and compute statistics(데이터 시각화 및 통계 계산)
첫 번째 방법은 데이터를 그려보는 것이다. plot을 그려서 decision boundary 같은 것을 표현할 수 있는지, 확인할 수 있다. 또는 mean(평균)이나 standard derivation을 계산할 수도 있고, 입력과 출력 사이의 상관관계를 계산할 수도 있다.
Performance metric - Root Mean Square Error

공통화된 성능 metric으로서 Root Mean Square Error(RMSE)을 계산할 수도 있다. 앞선 MSE의 경우 에러값을 제곱한 것이기 때문에 MSE에 루트를 씌워줄 수 있다. 이때 root를 씌워줬기 때문에 예를 들어 RMSE의 결과값이 1이라고 했을 때 y와 동일한 위치에서 평균적으로 1이 차이 나고 있음으로 받아들일 수 있다.
Visualization

residual plot를 이용하여 정답값과 예측값 간의 차이를 그려볼 수 있다. 이때, 값의 차이에 추가적인 계산 없이 그대로 plot을 그려봤을 때, 0이 나오는 것이 최적이지만 0에서부터 얼마나 벗어났는지를 확인할 수 있다.
'Computer Science > 데이터 과학(Data Science)' 카테고리의 다른 글
| [데과/DS] Data Understanding & Visualization (0) | 2024.04.29 |
|---|---|
| [데과/DS] Regular Expression (정규 표현식) (1) | 2024.04.28 |
| [데과/DS] Data Acquisition (데이터 취득) (0) | 2024.04.28 |
| [데과/DS] Data Science Methdology (0) | 2024.04.26 |
| [데과/DS] Introduction to Data Science (2) | 2024.04.25 |