Neural networks (NN)
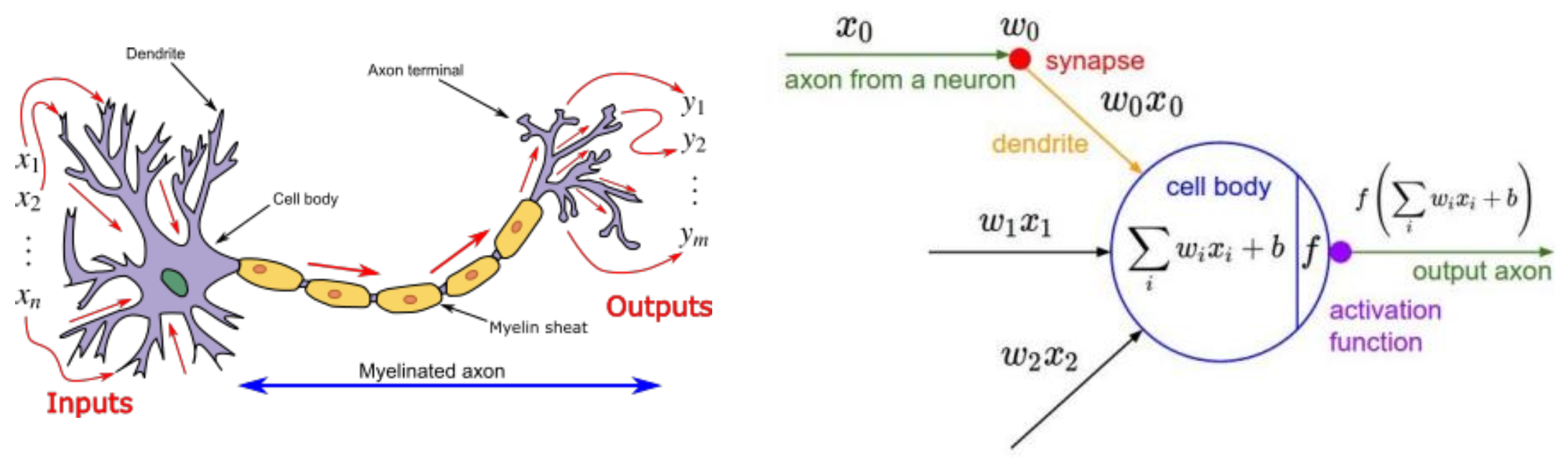
Neuron은 우리 몸의 신경 전달 물질이다.
NN은 이러한 뉴런을 모방하여 입력이 들어왔을 때, 입력이 각각의 뉴런을 통과하는데 통과하면서 어떤 weight를 곱하게 되고, 곱한 값이 일정 값(threshold) 이상인 경우 node가 activate되어 다음으로 값을 전달하고 작은 값은 무시한다.
Classification problem
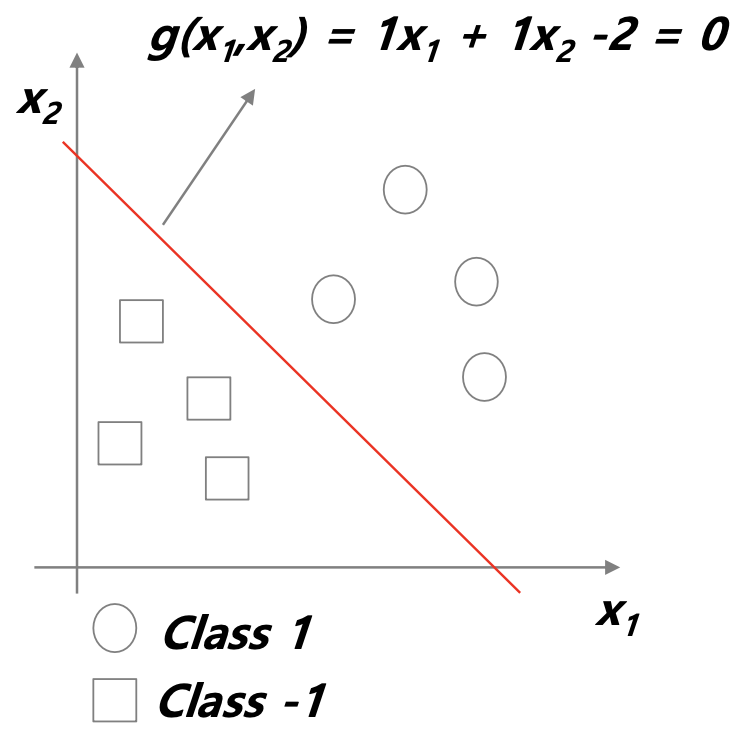
이진분류 문제를 통해 예를 들어보자.
위 사진과 같이 어떤 선을 기준으로 두 개의 클래스를 분류할 수 있으면 linear seperate를 가진다고 한다.
따라서 이러한 어떤 linear 함수를 통해 두 클래스가 쉽게 분리되는 문제에 대해 함수를 어떻게 둘 것인지에 대한 고민을 할 수 있다.
함수를 g라고 하면 이 g는 x1과 x2에 대한 함수이다. g는 linear 함수이므로 g(x1, x2) = w1x1 + w2x2 + w0의 식으로 나타낼 수 있을 것이다. 이때, w값에 대해 그래프의 모양이 결정되고 나서 g에 입력을 넣었을 때, 값이 0보다 작으면 -1, 0보다 크면 1이 되므로 0이 decision boundary가 된다.

따라서 이러한 식을 뉴런을 모방한 모델의 형태로 표현해보면 위 사진과 같다.
어떤 입력에 대해 각 weight를 곱하고, 그 결과값을 w0값과 더한 후 0을 기준으로 1과 -1의 값을 내는 함수를 통과함으로써 결과값을 낸다.
Linear machine
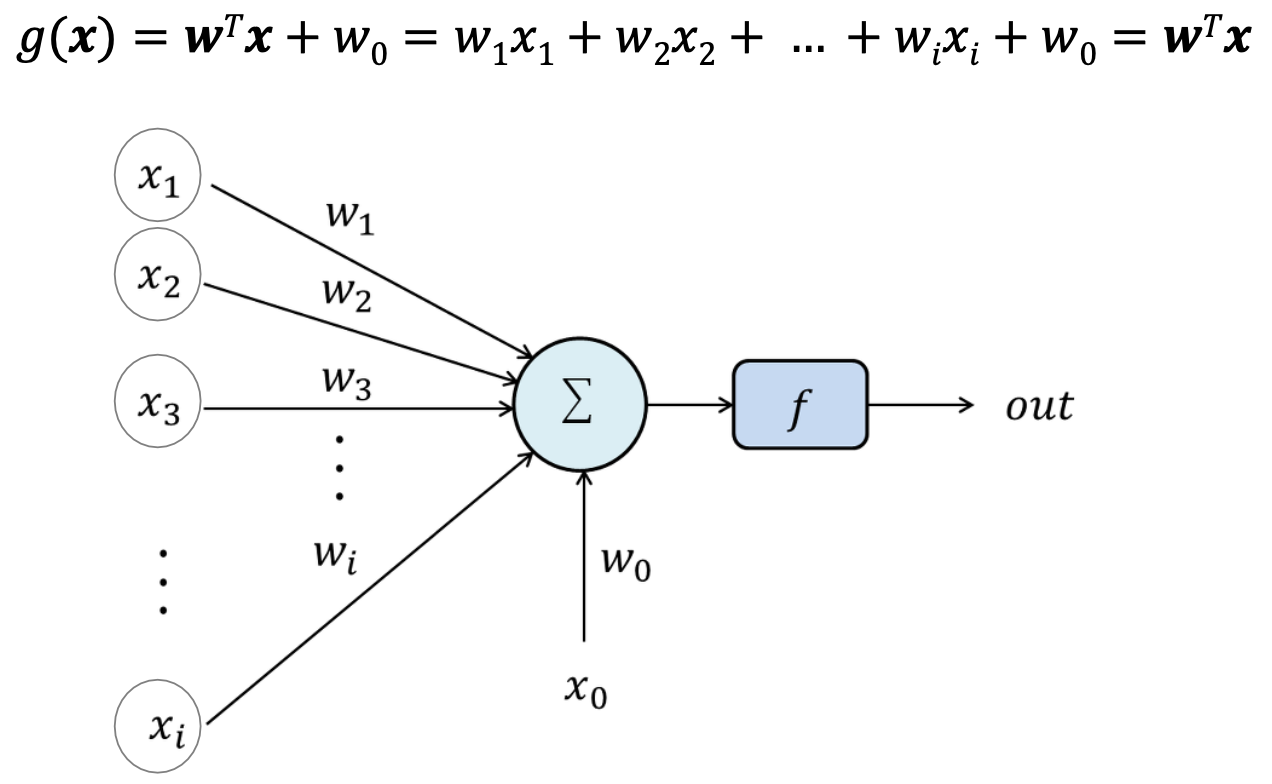
위와 같은 이진 분류에서 입력이 더 많아지면 위 사진과 같이 나타낼 수 있다.
선형식을 통해 각 weight를 곱하고 bias(w0)을 더해준다.
이때 x0은 X와 w의 내적을 위해 넣어둔 값으로 x0의 값은 항상 1이다.

이때, 각 용어는 사진과 같다.
입력값은 input variables라고 하며, 입력값이 거치는 동그라미를 node, node에서 node로 이동하기 위해 곱하는 값을 weight, decision boundary를 기준으로 활성화 여부를 결정해주는 함수를 activation function이라고 한다.
Perceptron
사람의 신경망을 모방한 인공지능에 대한 연구는 1957년도부터 시작되었다.
하지만 당시의 컴퓨터 성능이 뛰어나지 않아 주목을 받지 못하고 있다가
2010년대부터 HW의 성능이 높아지며 다시금 주목을 받게 되었다.
Activation function
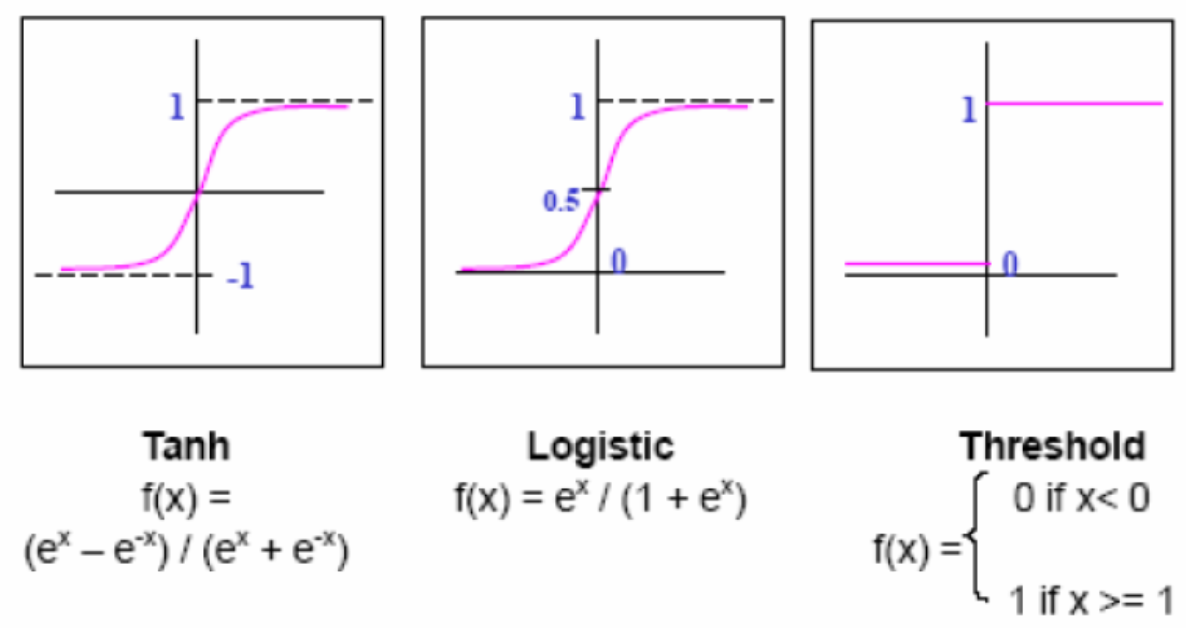
Activation function의 역할은 앞에서 들어온 weighted sum 형태의 입력을 가공하여 출력하는 것이다. 다양한 종류가 있지만, 이 중에서 sigmoid가 가장 실제 뉴런의 모습과 비슷하여 현재는 sigmoid를 자주 사용하지만 이 외에도 다른 활성 함수도 자주 사용되고 있다.

간단한 예시를 보자.
위 사진에서 3개의 데이터가 존재하고, 1번이 동그라미, 2번 3번이 네모라는 클래스를 갖고 있다고 하자.
이때, 각 값에 대해 어떤 활성함수를 사용하냐에 따라 다른 값을 출력하고 있음을 알 수 있다.
Multilayer Perceptron (MLP)

위와 같이 1개의 perceptron을 사용하는 경우는 linear seperate를 가지는 경우이다.
하지만 사진과 같이 XOR 문제의 경우 linear seperate하지 않다.
따라서 더 복잡하거나 non-linear classification의 경우 하나의 perceptron으로 문제를 해결할 수 없기 때문에 perceptron을 여러 개 쌓는 multi-layer perceptron이 도입된다.

multi-perceptron을 통해 XOR 문제를 풀어보자.
각각의 weight와 bias를 사진과 같이 둔다.
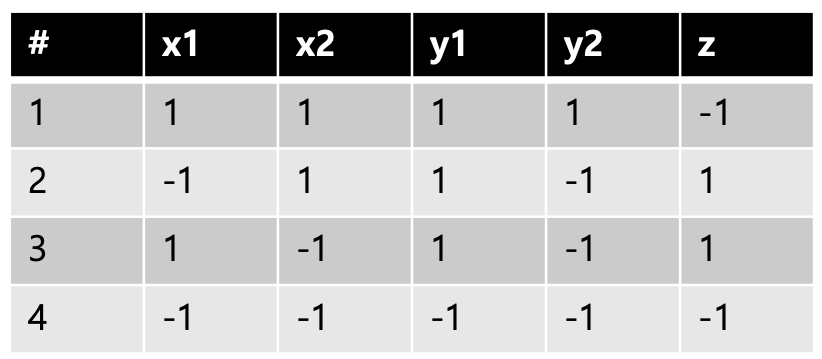
각각의 노드를 통과한 값은 위 표와 같다.
노드를 통과할 때 활성함수도 함께 통과하기 때문에
0보다 크면 1, 0보다 작으면 -1의 값이 나오게 된다.
따라서 결과를 보면 XOR의 결과와 동일하게 나오고 있음을 확인할 수 있다.
Universal approximation theory
일반적인 어떤 universal한 또는 nonlinear한 문제를 multi-perceptron을 통해 근사할 수 있다. 즉, perceptron을 여러 개 두면 어떠한 nonlinear classifier 문제를 풀 수 있다.
Feedforward vs. Backpropagation
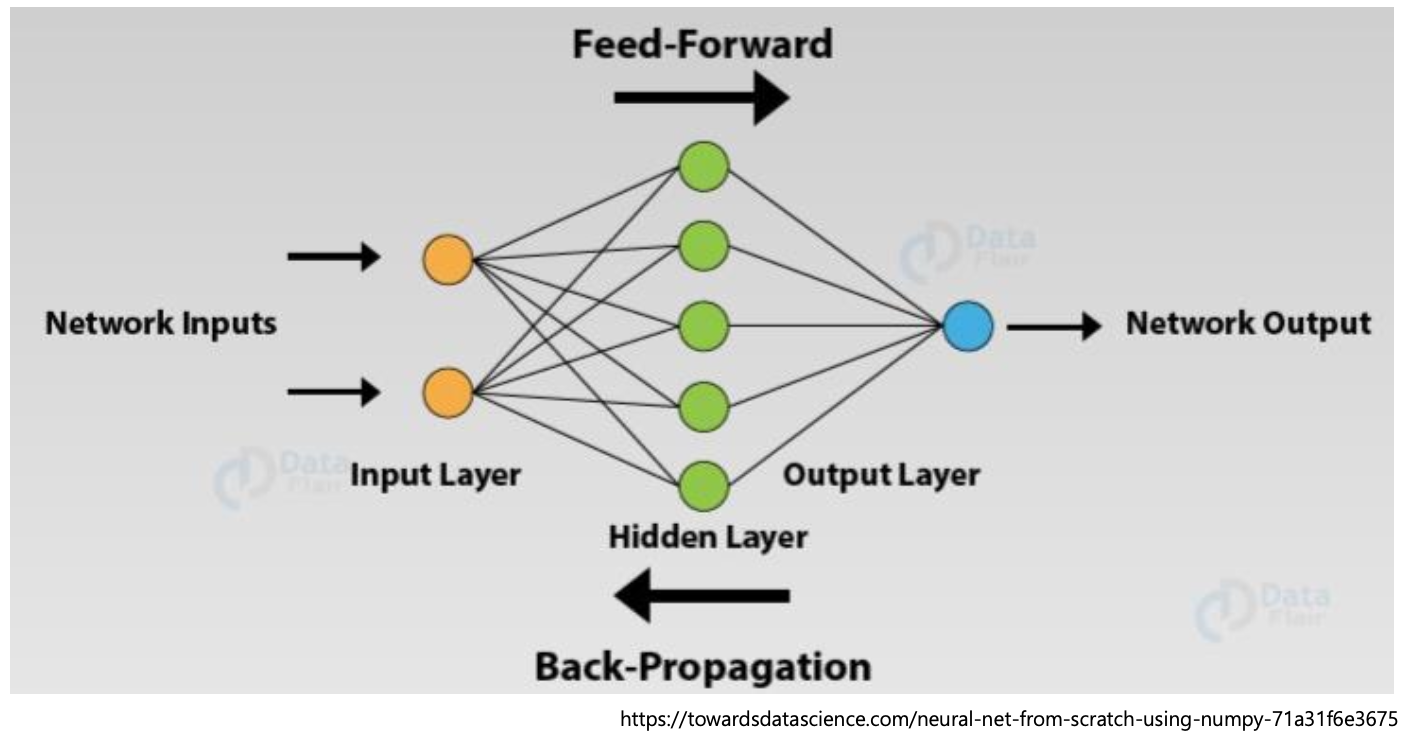
ML은 데이터를 통해 학습하는 과정이다. 따라서 우리는 데이터를 통해 weight와 bias를 학습시켜야 한다.
위 사진에서 input layer에서는 입력 feature가 2개고, output node가 한 개 있는데, 이 두 layer 사이에 있는 모든 layer는 hidden layer라고 한다. 왜냐하면 input-output의 관계에서 보이지 않는 연산을 하고 있기 때문이다.
이때 input -> output의 layer 방향으로 데이터가 타고 흐르는 경우를 feed-forward라고 한다.
반면 output과 실제값을 비교하여 오차를 계산하여 weight에 반영(update)하는 과정을 backpropagation이라고 한다. 즉, weight의 학습 과정인 것이다.
가장 초기의 weight 값은 임의의 값으로 지정한다. 이후 모델에 데이터를 통과시켜 weight를 조정하고, 또 새로운 데이터를 넣은 후 weight를 조정하는 과정을 반복하여 weight를 학습한다.
즉, feed-forward와 backpropagation의 과정을 반복하면서 weight를 학습시킬 수 있다.
Feedforward Process (Multiplayer perceptron)
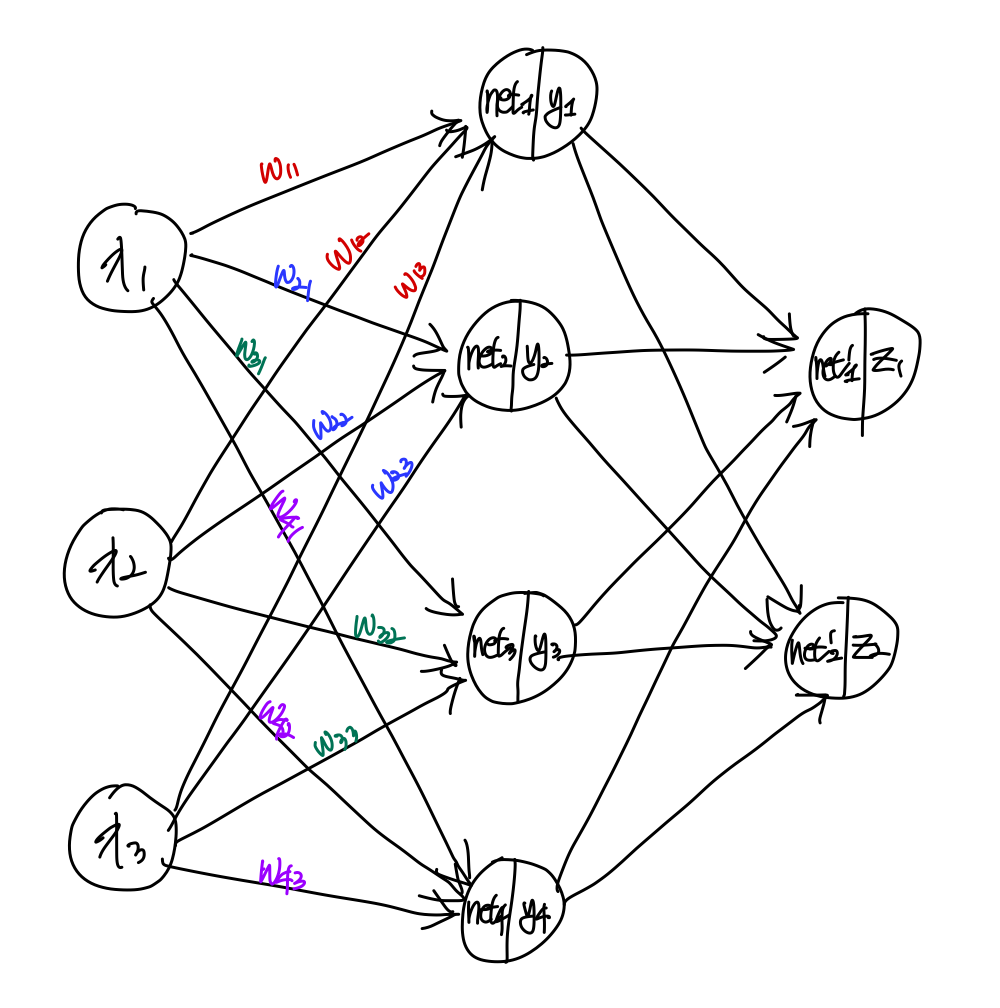
위 그림은 multi-perceptron을 나타낸 그림이다.
각 노드에는 bias가 존재하고, 입력의 모든 합인 net과 활성화함수를 통과한 y값이 존재한다.
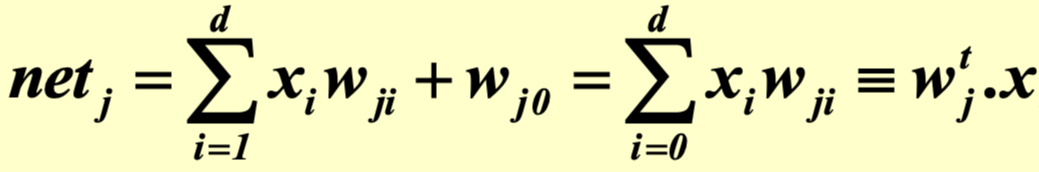
따라서 net을 구하는 식은 위와 같다.
이때, wj0은 bias의 값이고 x0은 1이다.
마찬가지로 yi, zi의 경우네는 f(neti)라고 표현할 수 있는데,
이때 f는 활성함수를 의미한다.

따라서 g는 위와 같이 나타낼 수 있는데,
이때 k는 k번째 output이라는 의미이다.
NN structure
# of hidden layers/nodes
입력 노드의 개수는 입력하는 데이터의 feature 개수이고,
출력 노드의 개수는 문제의 형태의 따라 클래스의 개수 등으로 나타낸다.
그렇다면 우리는 hidden layer의 층이나 노드의 개수에 대해 결정해야 한다.
이때, layer나 node의 개수가 많아지면 capacity가 커져 overfitting 될 가능성이 높아진다.
activation function
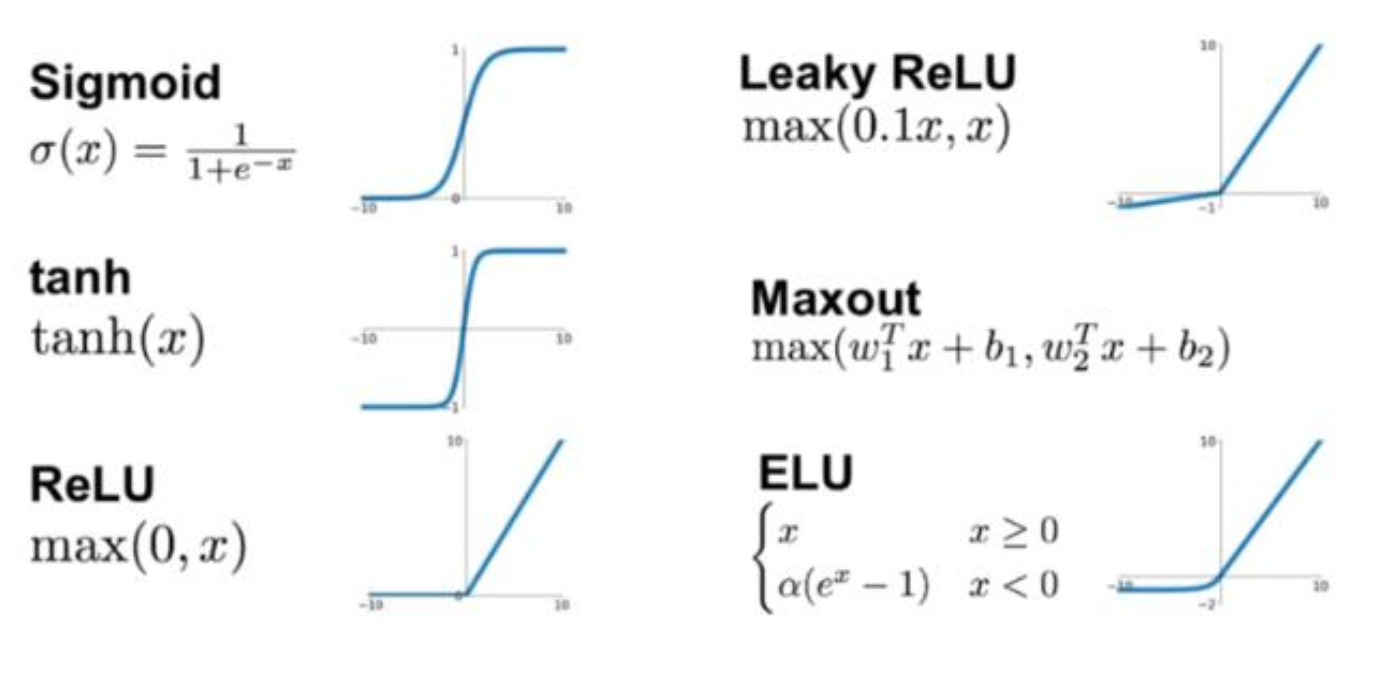
- sigmoid
전기자극 실험의 결과로 가장 유사하게 나온 sigmoid가 있다.
그러나 값의 범위가 0 ~ 1 사이라는 점으로 인해 값이 shift되는 문제 있다.
- tanh
위의 단점으로 인해 값의 범위가 -1 ~ 1인 tanh 함수를 사용할 수 있다.
RNN에서 주로 사용한다.
이때 sigmoid와 tanh의 경우 propagation을 통해 값을 구할 때 미분값으로 어떤 결과를 구하여는 경우 기울기가 0이 되는 지점이 두 군데나 존재하기 때문에 이러한 문제를 방지하고자 ReLU가 등장하였다.
- ReLU
Rectified Linear Unit의 약자로, 입력이 음수일 때는 0, 양수일 때는 그 값을 그대로 출력해주는 함수이다. 이 함수는 sigmoid처럼 값이 shift 되지도 않고, 미분값이 음수에서는 0, 양수에서는 1이라는 아주 직관적인 값을 가지고 있기 때문에 현재까지도 자주 사용하는 활성 함수이다.
- Leaky ReLU
ReLU의 변형으로 음수인 경우 해당 노드 값이 0이 되기 때문에
다음 노드에 대해 제대로 학습이 되지 않는다는 단점이 존재한다.
따라서 약간의 기울기를 조정하여 음수인 경우 입력값에 0.1을 곱해 기울기가 천천히 증가하도록 하는 Leaky ReLU도 사용할 수 있다.
- ELU
양수인 경우 해당 값을 그대로 출력하는 것에 비해, 음수인 경우 지수 함수의 느리게 증가하는 특정 부분을 이용하는 활성함수도 존재한다.
활성 함수 사용에 대해서 정해진 것은 없고, 적절한 값이 들어오면 해당 값을 활성 함수를 통과한 값으로 돌려주기만 하면 된다.
Role of activation function in hidden unit
input과 hidden node의 weight sum 관계는 행렬의 곱으로 표현할 수 있다.
이때 활성 함수도 행렬곱의 형태로 표현이 된다면 input과 output의 관계가 행렬의 곱으로만 표현될 수 있다. 이때, 중간 행렬을 축약하면 하나의 행렬로도 표현을 할 수 있다.
그런데 input과 output의 관계가 하나의 행렬로 표현된다는 의미는 linear transfomation 단계까지만 갈 수 있다는 의미이기 때문에, weighted sum으로 활성 함수를 통과시켜 non-linear transformation의 형태로 만들어 준다.
따라서 활성함수는 hidden node에서 모델을 non-linear transformation으로 만들어주는 역할을 한다고 할 수 있다.
Activation function for output units
활성함수는 hidden node에서 non-linear transformation으로 만들어 주는 역할을 한다고 하였다.
이때, output layer에 대해서 활성함수는 결과값을 출력해야 한다.
우리가 어떤 결과값을 기대하냐에 따라 사용하는 활성 함수의 종류가 바뀐다.
아래 몇 가지 예시를 보자.
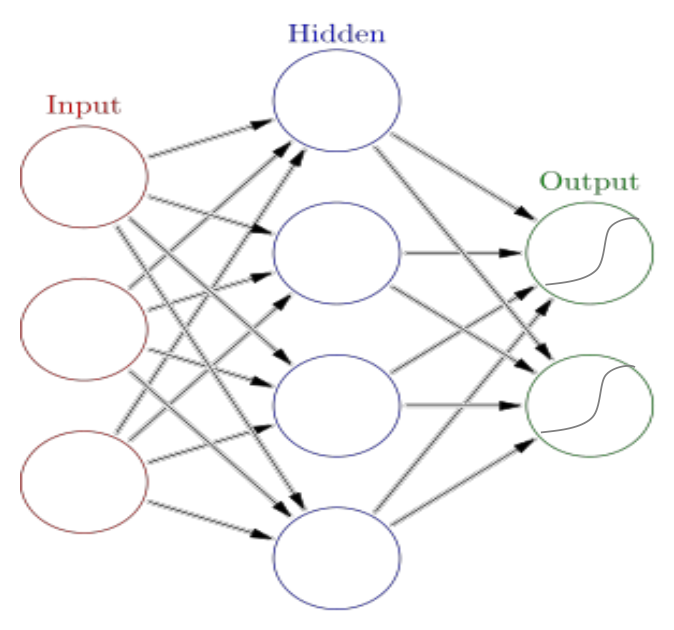
위 예시는 2개의 클래스, 즉 binary인 경우에 대해 분류하는 문제이다.
binary의 경우라면 output layer에서 sigmoid를 사용해도 된다.
이때, output layer의 node가 2개가 존재하는데, 이는 N-class의 경우와 형태를 맞춰주기 위함이다.
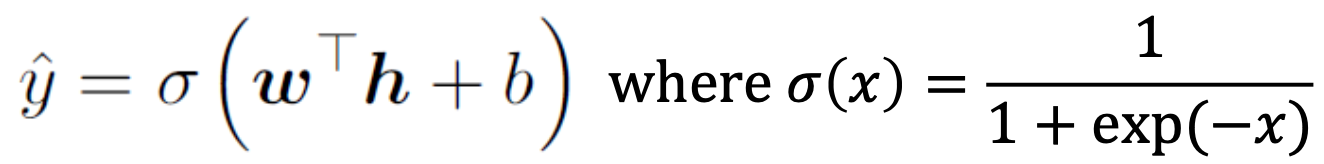
따라서 결과값이 [1 0], [0 1]의 형태로 클래스를 분류할 수 있다.
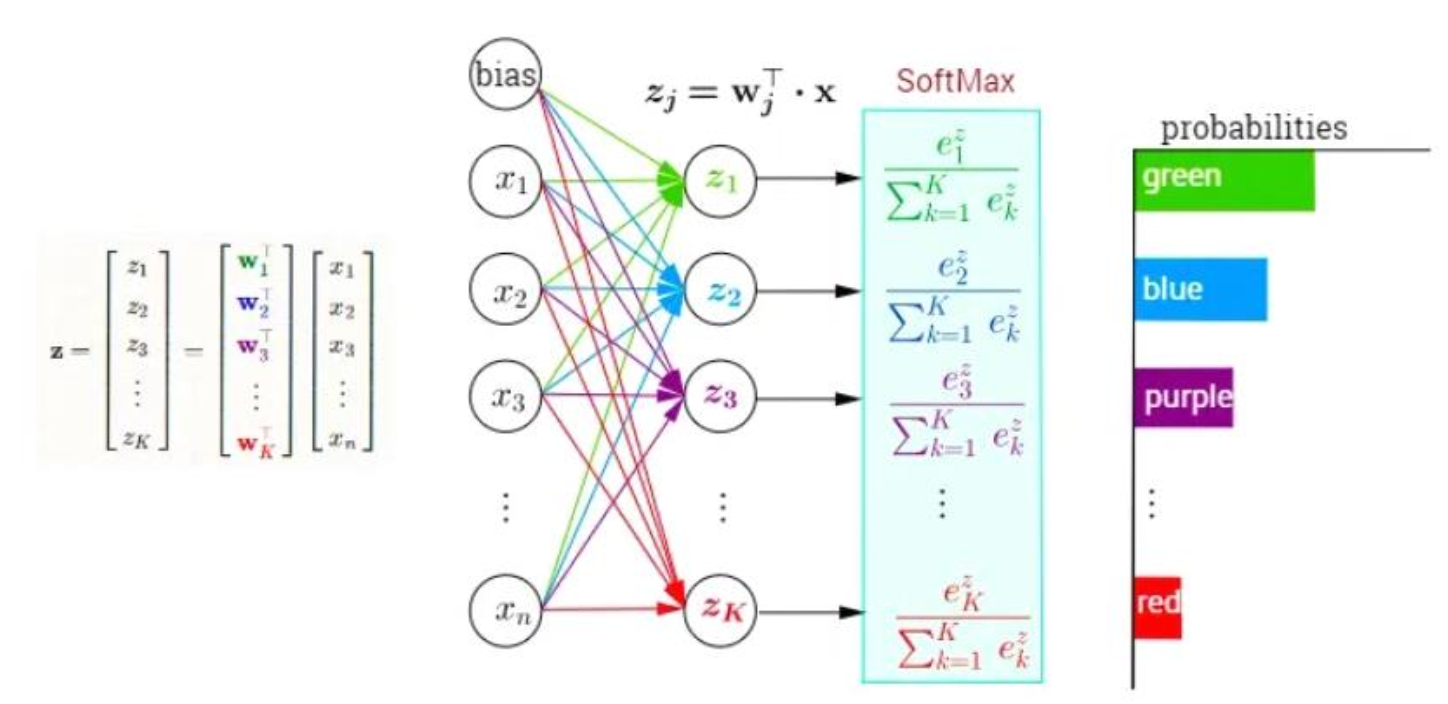
위 예시는 Multi-class에 대한 분류 문제로, 분류해야 하는 클래스의 개수가 3개 이상인 경우를 말한다.

이와 같은 경우 보통 softmax 함수를 주로 사용한다.
예를 들어 출력값 y가 [1 0 0 0]인 경우 예측값이 [0.8 0.1 0.05 0.05]와 같이 각 클래스에 속할 확률을 구함으로써 분류를 진행할 수 있다.
위 예시는 regression에 대한 문제로 실수값을 출력하면 된다.
따라서 input feature의 개수에 따라 input layer의 node 개수가 정해지게 되고, hidden layer와 node는 자유롭게 구성할 수 있다. hidden node activation function의 경우 non-linear한 함수의 형태로 정하면 되고, output layer의 node인 경우 원하는 출력값의 형태에 따라 activation function을 설정함으로써 모델을 설계할 수 있다.
Loss function
이제 실제값과 예측값 사이의 오차를 구해 loss function을 정의할 수 있다.
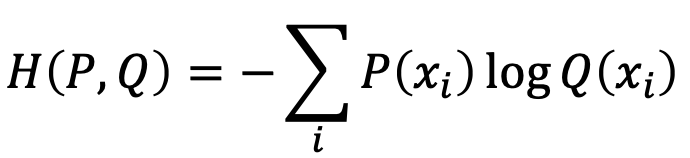
classification의 경우 cross-entropy를 사용하여 loss function을 구해줄 수 있다.

마찬가지로 regression의 경우 MSE를 사용하면 되는데, 나중에 미분할 것을 대비하여 제곱을 한다.
Feedforward process
Feedforward process의 예시를 보자.
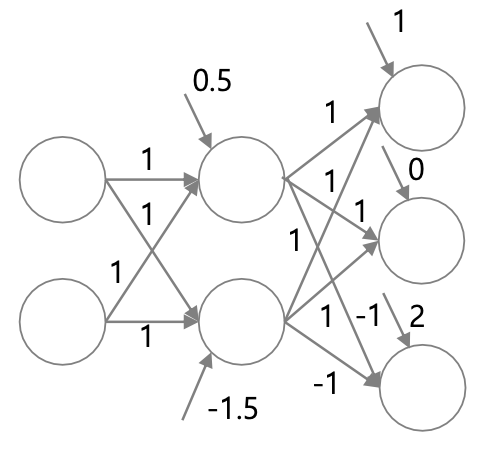
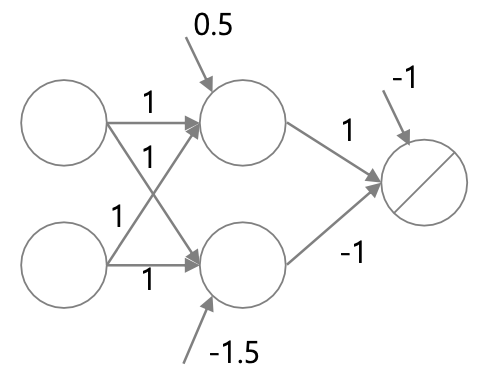
위 사진과 같은 모델이 있다고 했을 때, hidden layer에서는 ReLU 활성함수를 사용하고, output layer에서는 softmax 활성함수를 사용한다고 하자.

입력이 [1 0]일 때 실제값은 [1 0 0]이고, [0.83 0.14 0.03]이라는 예측값이 나왔다고 하자.
(임의의 값이며 값은 정확하지 않다.)
이때 classification이므로 cross-entropy를 통해 loss를 계산할 수 있다.
각 값에 cross-entropy식을 대입하면
-(1*log(0.83) + 0*log(0.14) + 0*log(0.03))이므로 loss는 결국 -log(0.83)이 된다.
Backpropagation - Training of MLP
우리는 Backpropagation 시 loss 계산 이후 weight를 업데이트 해준다.
이때, loss를 줄이기 위해 우리는 gradient descent 방법을 사용한다.
즉, loss에 대한 편미분 값을 계산해 주는 것이다.
이를 통해 loss를 줄일 수 있는 방향으로 weight를 업데이트 할 수 있는데,
각 업데이트된 weight 값은 편미분 값에 learning rate를 곱한 값이다.
따라서 feed-forward process의 경우 입력에 대한 output으로 최종 loss를 실제값과 비교하는 과정이고, backpropagation은 loss를 줄이기 위해 weight를 어떻게 업데이트를 해야 하는 지에 대한 계산 과정이라고 할 수 있다.

위 사진에서 w1,1을 업데이트 한다고 하자.
우리는 (learning rate)*(loss function)을 w1,1에 대해 편미분한 값을 통해 gradient descent를 진행한다.
이때 w1,1에 대해 미분하는 것은 쉽지 않은 일이다.
왜냐하면 결과값은 많은 hidden node를 거치며 weight를 곱해진 값에 활성함수까지 거쳤기 때문에, 타고 들어가야 하는 식들이 많기 때문이다.
그러나 우리는 output에 대한 미분이 weight sum에 대한 미분 등을 먼저 진행해줄 수 있다. 따라서 w1,1에 대한 편미분을 구하기 위해 output으로부터 w1,1까지 순차적으로 편미분을 구하면 쉽게 구할 수 있다.
이렇게 뒤에서 전파하는 알고리즘이라고 해서 backpropagation(역전파)이라고 한다.
Example
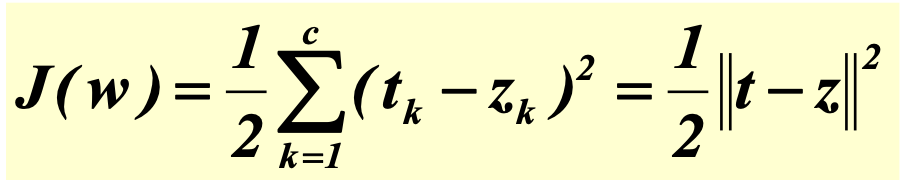
에서

일 때,

위와 같은 식이 된다.
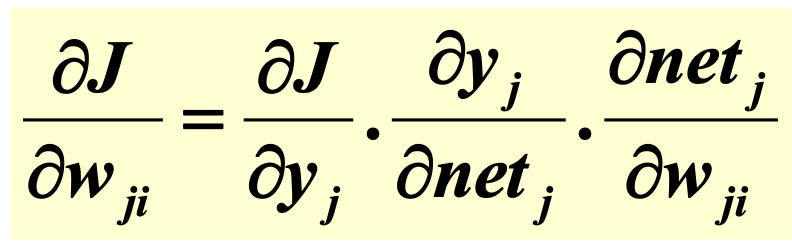
따라서 위 식에 대해

위와 같이 나타낼 수 있다.
Learning rate
learning rate는 업데이트할 양을 정해준다.
learning rate 값이 큰 경우 원하는 local optimum에 도달하지 못하고 발산하거나 주변에서 계속 머무르는 형태를 띤다. 반면 learning rate 값이 작은 경우 학습 속도가 더뎌져 많은 연산을 해야 하거나, 최적의 기울기에 도달하지 못하게 된다.

learning rate를 적절히 설정하는 경우 적당한 값에 잘 도착할 수 있다.
Local optima problem

우리가 사용하는 방법은 gradient descent 기반이기 때문에 최적의 해를 찾아갈 때 어떤 함수의 global minimum 값이 아니라, local optimum에 도달할 수 있게 된다.
이때, global minimum에 도달할 수 있는 방법은 수학적으로 존재하지 않기 때문에 gradient descent만의 문제가 아니다.
'Computer Science > 기계학습 (Machine Learning)' 카테고리의 다른 글
| [기계학습/ML] Deep Neural Networks (1) | 2023.12.18 |
|---|---|
| [기계학습/ML] Ensemble Method (1) | 2023.12.17 |
| [기계학습/ML] Decision Tree (1) | 2023.12.17 |
| [기계학습/ML] Bayesian Classifier (1) | 2023.10.23 |
| [기계학습/ML] Introduction to ML (2) | 2023.10.23 |