암호(cryptography) 기초 용어
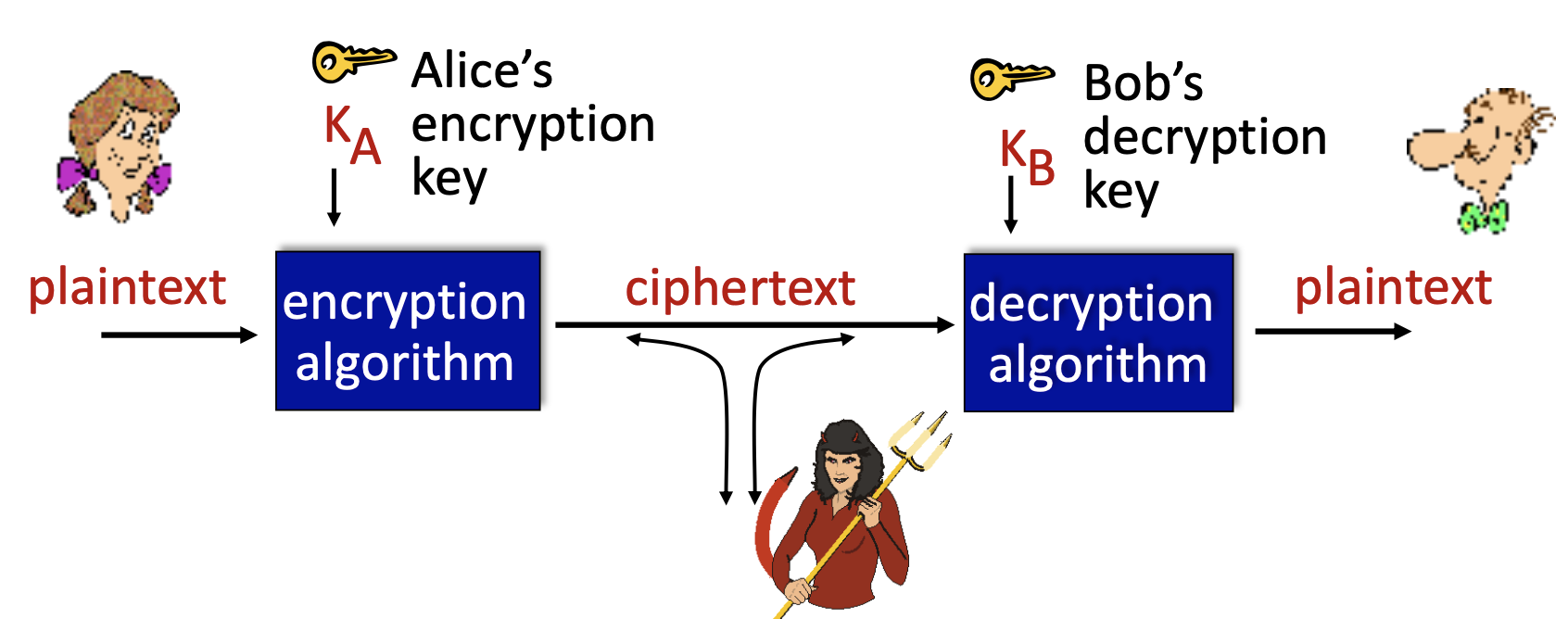
- m: plaintext message (평문)
- KA(m): ciphertext (암호문), 키 KA로 암호화
- m = KB(KA(m)) -> 복호화
암호 깨기
암호문을 전문적으로 깨는 방법(cipher-text only attack)이 존재하는데, 두 가지의 접근 방법이 있다.
- brute force
무차별 대입법이라고도 불리는 이 방법은 말 그대로 나올 수 있는 경우의 수들을 모두 대입해보는 방법이다.
- statistical analysis
통계적 분석 방법은 쓰이는 알파벳이나 단어들을 우선적으로 대입해보는 방식이다.
그 외에도 아래와 같은 방법이 존재한다.
- known-plaintext attack
공격자가 평문(plaintext)과 암호문(ciphertext)을 모두 가지고 있을 때 사용할 수 있는 암호 해독 기법들을 말한다.
- chosen-plaintext attack
공격자가 임의의 plaintext에 대한 ciphertext를 얻을 수 있다고 가정하는 암호 해독 공격 모델이다.
Symmetric key cryptography (대칭키 암호화)

대칭키는 송신자와 수신자가 대칭되는 키를 통해 암호화/복호화를 진행할 수 있다.
예를 들면, 알파벳으로 작성된 데이터를 암호화 방법으로 각 알파벳을 왼쪽으로 한 칸씩 이동하는 방법을 사용했다면, 복호화할 때는 각 알파벳을 오른쪽으로 한 칸씩 이동하는 방법을 이용하여 원문을 알아낼 수 있는 것이다.
이때, 알파벳을 왼쪽으로 한 칸씩 이동했다와 같은 키를 수신자에게 그대로 전송하면 안 되기 때문에 암호화를 진행하는데 이때 보통은 Diffie-Hellman(DH) 알고리즘을 통해 키를 전달한다.
substitution cipher
초기에 사용하던 암호화 방식으로, 글자 하나를 다른 글자로 치환하여 전송한다.

이때 monoalphabetic cipher라는 방법도 존재하는데, 위의 방법과 거의 비슷하다.
위와 같은 방식은 통계적 분석과 같은 방식으로 쉽게 키를 찾아낼 수 있다.
따라서 위의 방법을 조금 더 심화하여 N개의 매핑 블럭을 만들고 번갈아가며 대치시키는 방법도 사용할 수 있다.
예를 들어 n = 4일 깨, M1, M2, M3, M4의 블럭을 만든다. 이후 M1, M3, M4, M3, M2; M1, M3, M4, M3, M2; .... 과 같은 사이클 패턴을 통해 평문을 대치시킨다. 이후, dog라는 글씨를 전송할 때 d = M1, o = M3, g = M4로 각각의 매핑하여 암호화를 진행한다.
위와 같은 방법을 사용하여 더 안정하게 암호화를 진행할 수 있다.
Symmetric key crypto: DES
Data Encryption Standard의 약어로 가장 오래된 암호화 표준이다. 1993년 US의 암호화 표준으로 사용하였다.
입력으로 들어온 plaintext를 64bits의 단위로 쪼갠 후, 56bits의 대칭키를 통해 연산을 한다.
해당 알고리즘이 등장했을 때에는 암호화가 잘 되었으나 현재는 cpu의 발전으로 한 번에 진행할 수 있는 연산량이 많아지면서 하루 이내에 해독할 수 있다.
AES: Advanced Encryption Standard
대칭키 NIST 표준이다. 2001년에 등장하였으며 DES를 대체하게 되었다.
DES와 비슷한데, 입력으로 들어온 plaintext를 128bits로 끊고 암호화 시 128, 192 또는 256bits짜리 키를 사용한다.
DES에 비해 길이가 굉장히 길어졌으므로 부르트포스 알고리즘으로 계산하여도 현재 연산량으로는 몇 만년이 걸린다고 한다.
거의 대부분의 암호화 알고리즘은 이러한 방식으로 진행된다. 키를 길게 만들거나, 알고리즘을 복잡하게 만들어 모든 경우에 대한 출력이 오래 걸리도록 만든다. AES는 현재에도 우리가 사용하는 암호화 알고리즘 중 하나이다.
Public Key Cryptography (공개키)
공개키는 암호화/복호화 키가 서로 다르며 공개되는 키와 비공개키(개인키)가 쌍으로 존재한다. TLS로 데이터 송수신을 위한 인증서를 생산할 때 개인키와 쌍이 되는 공개키를 생성하고 이 키를 공개한다.
공유키는 암호화 시 사용하고, 개인키는 복호화 시 사용되며, 공개키로 암호화한 데이터는 개인키로 복호화가 가능해야 하며, 마찬가지로 개인키로 암호화한 데이터는 공개키로 복호화가 가능해야 한다.
이때, 개인키는 나를 증명할 수 있는 수단이 되므로 전자서명에서도 이러한 알고리즘을 이용한다.
공개키를 통해 개인키를 유도할 수 없어야 하므로 인수분해 알고리즘을 통해 어려운 키를 만든다. 따라서 계산하는 데에 오랜 시간이 들어 대칭키보다 느리다는 단점이 있다.
그런데, HTTPS에서 TLS를 통해 데이터를 전송할 때에는 공개키와 대칭키 모두 사용한다. 메세지, 즉 데이터를 암호화할 때에는 속도가 빠른 대칭키를 사용하고, 서버의 인증서나 키를 교환할 때에는 공개키를 사용한다.
공개키 사용 시 키를 교환하는 데에 가장 안전한 알고리즘은 DH 알고리즘이다.
대칭키 알고리즘에서 DH 알고리즘을 사용하긴 하지만, 보통은 공개키 알고리즘(RSA)에서 사용한다.
DH 알고리즘은 사용하면 키를 직접 공유하지 않고도 pre-master 키를 통해 키를 생성할 수 있는 시드값을 받아 각자 키를 계산한다. 이때 계산 결과는 서버와 클라이언트가 동일하다.
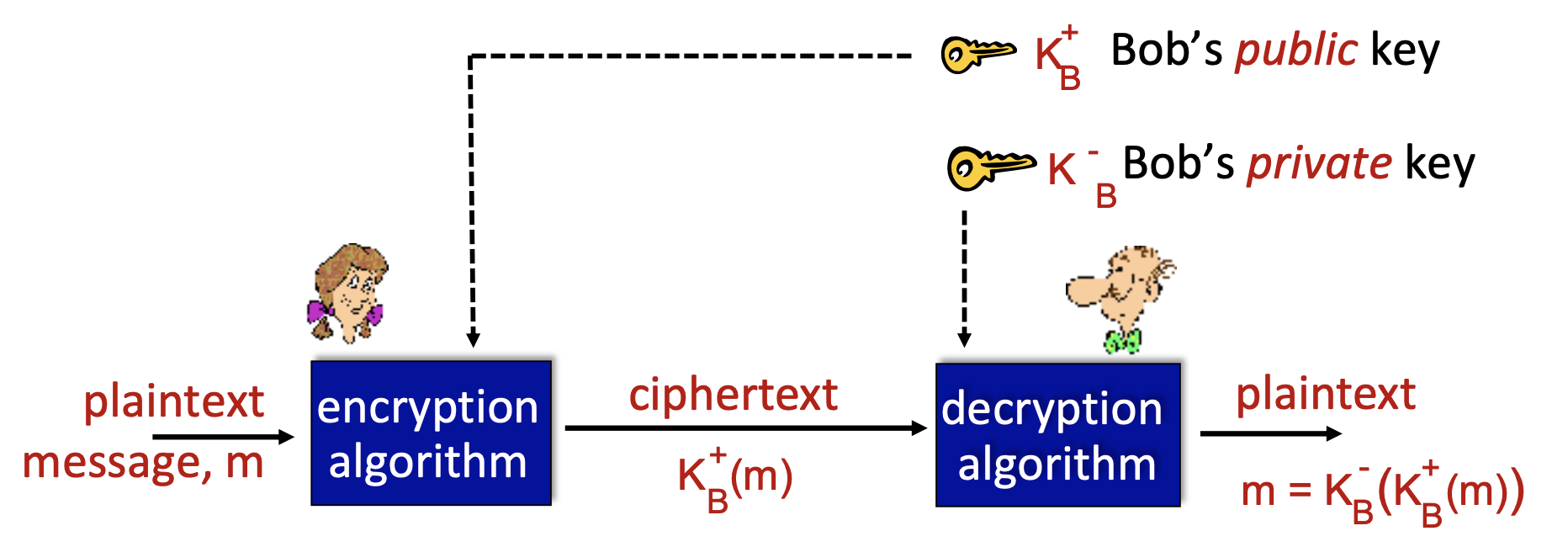
공개키 알고리즘을 사용하기 위해서는 아래 요건이 충족되어야 한다.
1. K+가 공개키, K-가 개인키라고 할 때, K-(K+(m)) = m의 식이 만족한다.
2. K+를 통해 K-를 유도할 수 없어야 한다.
RSA
RSA 알고리즘은 아래의 규칙을 따라야한다.

공개키를 통해 암호화한 후 개인키로 복호화를 하든, 개인키로 암호화한 후 공개키로 복호화를 하든 동일한 결과가 출력되어야 한다.
RSA 알고리즘의 암호화와 복호화 과정을 알아보자.
0. DH 알고리즘을 통해 암호화 키 (n, e)와 복호화 키(n, d)를 생성했다.
1. 메세지 m(<n)은 암호화를 위해 아래 식을 계산해야 한다.
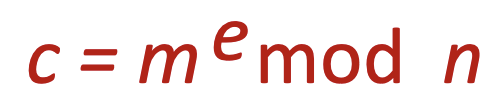
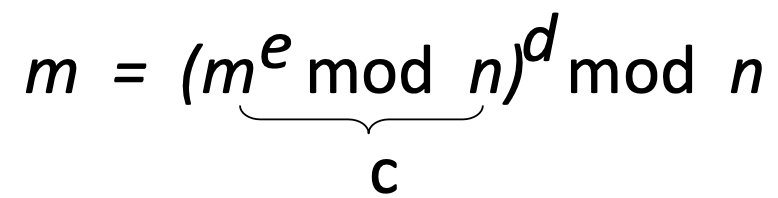
2. 수신된 비트 패턴을 복호화하기 위해 아래 식을 통해 c를 계산한다.

따라서 RSA 알고리즘을 아래와 같이 표현할 수 있다.
RSA: Creating public/private key pair
RSA 알고리즘으로 공개키와 개인키를 어떻게 생성하는지 알아보자.
1. 2개의 소수 p, q를 선택한다. 이때, p와 q는 큰 값이어야 한다.
2. n과 z를 구한다.
- n = pq, z = (p-1)(q-1)
3. z와 서로소(겹치는 소인수 x)인 값 e를 구한다. (e < n)
4. ed - 1를 z로 나누었을 때 나누어 떨어지는 값 d를 구한다. (ed mod z = 1, ed % z = 1)
5. 공개키는 (n, e)이고, 개인키는 (n, d)이다.
한 가지 예를 통해서 RSA 알고리즘을 적용시켜보자.
1. p = 5, q = 7라고 하자.
2. n = 5 * 7 = 35, z = (5 - 1)(7 - 1) = 4 * 6 = 24
3. e = 5, 24와 서로소
4. d = 29, (5 * 29 - 1)%z = 0 (하나하나 대입해서 구함)
5. 공개키는 (35, 5)이고, 개인키는 (35, 29)이다
RSA 알고리즘으로 암호화를 진행해보자.
식의 간소화를 위해 공개키 (n, e)는 (15, 3), 개인키 d는 3이라고 하자.
암호화 전의 평문 m = 2라고 하자.
암호화된 값은 c = 2^3 mod 15 = 8이다.
c값을 복호화해보자.
8^3 % 15 = 512 % 15 = 2로 암호화 전 값인 m과 동일한 값이 나온다.
디지털(전자) 서명
이러한 공개키의 장점으로 인해 우리는 전자 서명에서도 이 공개키 알고리즘을 사용한다.
은행과 같은 사이트에서는 해당 계좌에 접근하고 있는 사람이 진짜 나인지를 확인시켜줘야 한다.
따라서 나임을 증명하기 위해 아래와 같은 절차를 따른다.
1. 인증을 하기 위한 메세지 일부를 해싱한다.
2. 해싱된 결과를 개인키로 암호화한다.
3. 서버는 공개키를 통해 복호화를 진행하여 인증한다.
인증서
위의 과정으로 나를 증명할 수 있지만, 사이트는(공개키, 개인키 모두 보유) 나를 증명하는 것만으로는 해당 사이트를 신뢰할 수 있는지 알기 어렵다. 따라서 우리는 인증서를 통해 해당 사이트를 인증할 수 있다.
인증서는 정부나 은행같은 믿을 수 있는 기업에서 발급해준다.
인증서는 신원정보, 공개키, 유효기관, 인증기관정보, 인증기관의 전자서명을 포함한다.
Public Key Infrastructure (PKI): 상위(Root) CA + ... 하위 CA 트리구조
X.509
사용자, 컴퓨터, 서비스 또는 디바이스를 나타내는 디지털 문서이다.
CA(인증 기관), 하위 CA 또는 등록 기관에서 X.509 인증서를 발급한다.
이러한 인증서는 발급 시 .der 또는 .pem의 확장자를 가지고 있다.
인증서의 표준은 아래와 같다.
- certificate
version:인증서버전
serial number: CA가 할당한 고유번호
signature서명알고리즘식별자
issuer발행자(CA이름)
validity유효기간
subject소유자(domain)
subject public key info 소유자 공개키 정보
• public key algorithm
• subject public key
extensions
- certificate signature algorithm
- certificate signature
비대칭키와 인증서 만들기
인증서를 발급하는 명령어는 아래와 같다.
- 공개키의 개인키 만들기
openssl genrsa -out server.key 1024
genrsa는 rsa를 생성하겠다는 의미이다.
1024를 통해 개인키를 만든다.
- 인증서 요청 파일
openssl req -new -key server.key -out server.csr
- 인증서 만들기
openssl x509 -req -in server.csr -signkey server.key -out server.crt
x.509의 형태로 인증서 파일을 생성한다.
위 과정을 통해 server.crt 파일이 생성된다.
참고 및 출처
https://ko.wikipedia.org/wiki/%EA%B8%B0%EC%A7%80_%ED%8F%89%EB%AC%B8_%EA%B3%B5%EA%B2%A9
https://en.wikipedia.org/wiki/Chosen-plaintext_attack
https://www.nowwatersblog.com/cs/%EC%BB%B4%ED%93%A8%ED%84%B0%EB%A7%9D/8.%20Security
https://learn.microsoft.com/ko-kr/azure/iot-hub/reference-x509-certificates
'Computer Science > 컴퓨터네트워크(ComNet)' 카테고리의 다른 글
| [컴네/CN] 암호통신: 이메일 (0) | 2023.12.09 |
|---|---|
| [컴네/CN] 암호통신: 무결성 (1) | 2023.12.09 |
| [컴네/CN] 전송 계층 보안, TLS (1) | 2023.12.07 |
| [컴네/CN] IP Routing: BGP (2) | 2023.12.07 |
| [컴네/CN] IP Routing: RIP, OSPF (2) | 2023.12.07 |