FIRST의 한계
우리는 이전 포스트에서 FIRST에 대해 학습하였다.
하지만 이런 FIRST에도 한계가 존재한다.
A -> XXX와 같은 생성 규칙이 있을 때, non-terminal A가
nullale한 경우 문제가 발생하게 된다.
왜냐하면 FIRST만 가지고 생성 규칙을 결정적으로 선택할 수 없기 때문이다.
S -> Ab, S -> c, A -> ε의 경우
입력 문자열로 'b'가 들어온 경우 S -> Ab, 'c'가 들어온 경우 S -> c로 유도한다.FIRST(S) = {b, c}이기 때문이다.
하지만, 문법이 S -> Ab, S -> c, A -> a, A -> ε인 경우FIRST(A) = {a, ε}인데, FIRST(S) = FIRST(A) ⊕ FIRST(b)이므로
FIRST(S) = {a, ε} ⊕ {b} = {a, b}이다.
이때, 입력으로 'b'가 들어온 경우 S -> Ab를 선택할 수 있는데,A에서, a를 선택해야 할지, ε를 선택해야 할 지 모른다.왜냐하면, A의 FIRST에는 b가 존재하지 않기 때문이다.
따라서 A의 다음에 나오는 심벌에 따라 어느 생성 규칙으로 유도할 것인가를 결정해야 한다.
FOLLOW
FOLLOW
FOLLOW(A)는 시작 심벌로부터 유도될 수 있는 모든 문장 형태에서
A 다음에 나오는 terminal 심벌의 집합이다.
FOLLOW(A) = {a ∈ Vt ∪ {$} | S =>* αAaβ, α, β ∈ V*}
($는 입력 스트링의 끝을 표기하는 마커 심벌임)
모든 문장 형태를 고려하기 위해 생성 규칙의 rhs를 이용하여 FOLLOW를 구할 수 있다.
FOLLOW 계산 방법
(1) 시작 심벌 $는 초기 값을 갖는다.
FOLLOW(S) => {$}
(2) 생성 규칙 형태가 A -> αBβ, β != ε일 때, FIRST(β)에서 ε을 제외한 terminal 심벌을 B의 FOLLOW에 추가한다.
if A -> αBβ, β != ε then, FOLLOW(B) = FOLLOW(B) ∪ (FIRST(β) - {ε})
(3) A -> αB이거나, A -> αBβ에서 FIRST(β)에 ε이 속하는 경우(B => ε), A의 FOLLOW 전체를 B의 FOLLOW에 추가한다.
if A -> αB ∈ P or (A -> αBβ and β => ε) then, FOLLOW(B) = FOLLOW(B) ∪ FOLLOW(A)
Note)
생성 규칙 형태가 A -> αBβ인 경우, β가 ε이거나 또는 ε을 유도할 수 있으면, A의 FOLLOW 전체를 B의 FOLLOW에 넣는다. 왜냐하면, 임의의 문장 형태에서 A 다음에 나올 수 있는 심벌은 모두 B 다음에 나올 수 있기 때문이다.
S => α1Aα2 => α1αBβα2 or α1αBα2 (β가 nullable이기 때문)
FOLLOW 속성으로 인하여 A -> αB, B -> αA와 같은 형태의 생성규칙을 갖고 있으면 FOLLOW(A) = FOLLOW(B)이다.
첫 번째 형태의 생성 규칙으로부터 FOLLOW(A) ⊂ FOLLOW(B)이고, 두 번째 형태의 생성 규칙으로부터 FOLLOW(B) ⊂ FOLLOW(A)이기 때문이다.
이제 예제를 들어보자.
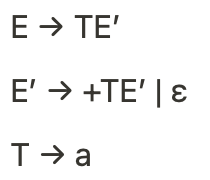
위의 문법에서 각 non-terminal의 FOLLOW를 구해보자.
가장 먼저 FIRST를 구하자.
FIRST(E) = {a}, FIRST(E') = {+, ε}, FIRST(T) = {a}
앞서 FOLLOW의 정의를 통해
(1)에서 FOLLOW(E) = {$}
(2)에서 FOLLOW(T) = FIRST(E') - {ε} = {+}
(3)에서
FOLLOW(E') = FOLLOW(E') ∪ FOLLOW(E) = {} ∪ {$} = {$}
FOLLOW(T) = FOLLOW(T) ∪ FOLLOW(E) ∪ FOLLOW(E') = {+} ∪ {$} = {+, $}
반복
FOLLOW(E') = {$} ∪ {$} = {$}
FOLLOW(T) = {+, $} ∪ {$} = {+, $}
더 변하지 않으므로
FOLLOW(E) = {$}, FOLLOW(E') = {$}, FOLLOW(T) = {+, $}
LL 조건
CGF가 임의의 생성 규칙 A -> α | β ∈ P에 대해 만족해야 할 조건이 있다.
1. FIRST(α) ∩ FIRST(β) = {}
2. if ε ∈ FIRST(α) then FOLLOW(A) ∩ FIRST(β) = {}
위의 규칙을 따르게 되면 생성 규칙의 FIRST에 공통 원소가 없으므로,
각 순간 적용할 생성 규칙이 유일하게(결정적으로) 결정된다.
또한 생성 규칙이 ε을 유도할 수 있으면 FOLLOW에 대해서도 고려해야 하므로FOLLOW와도 분리된 집합이어야 한다.
즉, LL 조건을 만족하는 문법은 ≈ LL 파싱되는 문법이다.
LL(1)문법
임의의 생성 규칙 A -> α | β ∈ P에 대해 LL조건을 만족하는 CFG이다.
('1') = lookahead가 하나임. 즉, 입력 토큰 하나만 보고 결정
위에서 언급한 LL조건에 따라 아래의 요소가 있는 CFG는 절대 LL(1)문법이 될 수 없다.
1. 모호한(ambiguous) CFG
2. left-factoring 될 부분을 갖고 있는 CFG
3. left-recursion한 CFG
지금부터 각각의 설명과 해결 방법을 설명하겠다.
LL문법이 되기 위해
모호성 해결
모호성은 우리가 앞 포스트에서 언급한 적이 있다.
간단히 넘어가자면, 모호성은 유도 트리가 두 가지 이상 나올 수 있는 경우이고
이 모호성을 해결하기 위해 같은 언어를 생성하는 다른 문법을 사용한다고 하였다.
해결하기 위해 연산자 우선 순위 추가와 결합법칙을 반영하는 방법을 사용한다.
Left Factoring
공통 앞부분(common prefix)을 새로운 non-terminal을 도입해 인수분해하는 것
A -> ab | ac ==> A -> aA', A' -> b | c
or
S -> iCtS | iCtSeS | a, C -> b
==> S -> iCtSS' | a, S' -> eS | ε, C -> b
Left Recursion
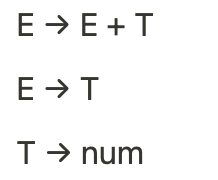
위와 같은 문법이 있다고 했을 때, 입력 문자열이 '1 + 2 + 3 + 4'이다.
아래는 유도 과정이다.

위와 같은 유도 과정은 문제가 있다.
왜냐하면 왼쪽으로 계속해서 non-terminal이 늘어나기 때문에
컴퓨터는 어디까지 늘어나야 하는지 알 수 없기 때문이다.
즉, 무한 loop의 가능성이 존재한다.
이러한 문제는 문법을 right-recursion로 만들어 해결한다.

left-recursion은 두 가지 방법으로 존재할 수 있다.
직접 left-recursion 제거
직접 left-recusioin은 A -> Aa의 형태를 말한다.
즉, lhs의 non-terminal이 rhs의 첫 심벌에 나타날 때, 아래와 같이 고칠 수 있다.
A -> Aa | b => A = Aa + b = ba*
=> A -> bA', A' => aA | ε

간접 left-recursion 제거
간접 left-recursion을 직접 left-recursion으로 변환하는 방법은 아래와 같다.
1. 일정한 순서로 non-terminal을 순서화한다.
2. lhs보다 순서적으로 앞선 non-terminal이 rhs의 첫 번째로 나타나는 생성규칙을 찾는다.
3. 대입을 해서 간접 recursion을 직접 recursion으로 바꾸어 준다.
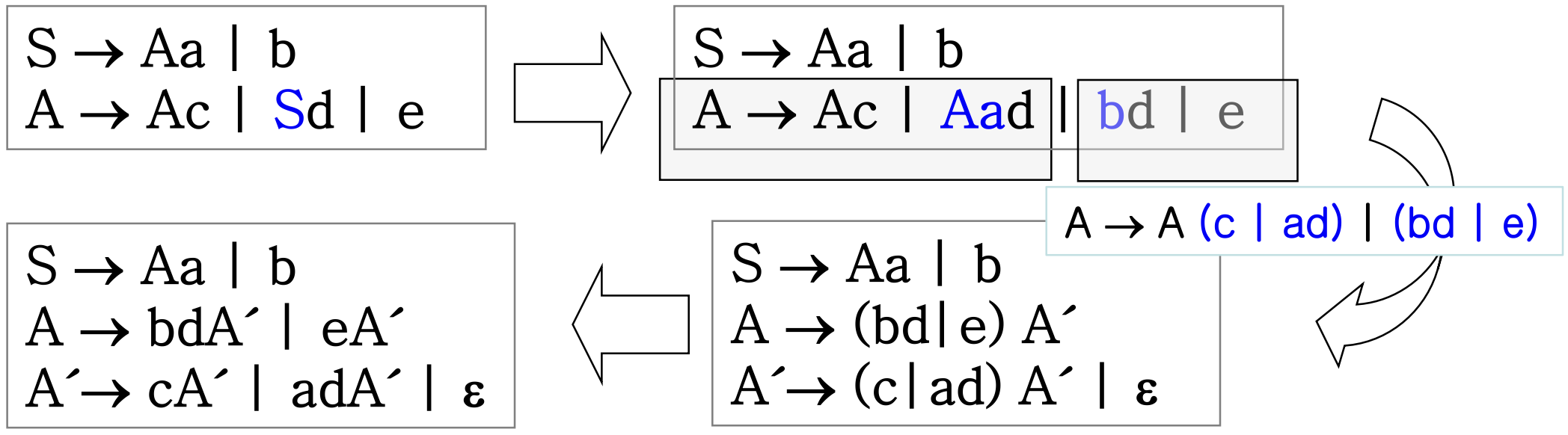
간단히 말하자면, 간접 recusion이 있는 non-terminal을 대입하여 없애주고,
left-factoring을 통해 인수분해 해주면 된다.
그래서, LL 문법은?
LL문법은 LL조건을 만족하는 CFG를 말한다.
주어진 문법에서 LL 문법을 구하는 방법은
1. 모호성 제거
2. left-factoring
3. left-recursion 제거
위 세 가지이다.
이후, LL 조건을 만족하는지 확인한다.
1. FIRST(α) ∩ FIRST(β) = {}
2. if ε ∈ FIRST(α) then FOLLOW(A) ∩ FIRST(β) = {}
그 다음 LL parsing한다.
LOOKAHEAD(...)
어떤 규칙을 적용했을 때 가장 처음 나올 수 있는 terminal symbols이다.
LOOKAHEAD(A -> X1X2...Xn)
= FIRST(X1) ⊕ FIRST(X2) ⊕ ... ⊕ FIRST(Xn) ⊕ FOLLOW(A)
Strong LL(1) 조건
임의의 택일 규칙 A -> a | b에 대하여 다음을 strong LL 조건이라 한다.
- LOOKAHEAD(A -> a) ∩ LOOKAHEAD(A -> a) = {} (공집합)
- 주어진 상황에서 LOOKAHEAD가 unique하게 결정
(LL(1)과 동일함)
'Computer Science > 컴파일러개론(Compiler)' 카테고리의 다른 글
| [컴개/CI] Bottom-Up 구문 분석, Shift와 Reduce (2) | 2023.10.22 |
|---|---|
| [컴개/CI] Top-Down 구문 분석, 구문분석기 만들기 (0) | 2023.10.21 |
| [컴개/CI] Top-Down 구문 분석, LL파싱과 FIRST (0) | 2023.10.20 |
| [컴개/CI] 구문 분석 방법 (0) | 2023.10.20 |
| [컴개/CI] 모호성(Ambiguity) (0) | 2023.10.20 |